- Messaggi: 850
- Ringraziamenti ricevuti 118
-
-

- Il Paranormale esi...
- Volano, io non mi preoccupo: l'arma se c'è, ce l'ha l'Iran. Il problema ci sarebbe stato se l'arma...
- da Mig25
- 16/04/2024 21:43
-
-
-

- LA GRAN TARTARIA E...
- @Nomit Mai sentito, mi spiace. Siccome gli edifici "neoclassici" sono una parte fondamentale della "Gran...
- da chgall
- 15/04/2024 22:38
-
-
-

- Film consigliati
- Assolutamente consigliato è anche "La terra dei figli", di quel bravissimo regista che è Cupellini....
- da unflownsky
- 15/04/2024 12:08
-
-
-

- Opinioni sul Docum...
- Guardando agli ultimi decenni con il senno di poi ha senso prendere in considerazione questo documentario o...
- da FabioBros
- 15/04/2024 11:26
-
-
-

- CDS y MMS. Qualcun...
- Grazie de la risposta Penelope. Ne aprofitto per uppare il post.
- da lysmata
- 13/04/2024 22:19
-
-
-

- Prove di censura n...
- Indubbiamente anche quella testa di condominio e i suoi seguaci hanno il diritto di esprimersi, ma siccome...
- da Mig25
- 12/04/2024 11:39
-
-
-
- Voci della Confede...
- Sul sito creato dal gruppo L/L Research sono state pubblicate (e vengono costantemente aggiornate) le...
- da Dipende
- 11/04/2024 10:35
-
Il soffitto di Micerino
Non saprei a chi rivolgermi per rendere pubblica la scoperta, credo che gli unici possibili interessati nel mondo accademico potrebbero essere proprio gli storici della matematica. Nel caso comunque citerei tutti i partecipanti alla discussione, più ne siamo più ci divertiamo.Rox2 ha scritto: Se hai modo di divulgare la scoperta, al di fuori di LuogoComune, decidi tu se farlo o meno.
Io non ho fatto nulla; se non era per te, l'avevo presa per parabola.
Qualora decidessi di farlo, non merito nessuna citazione; puoi chiamarmi semplicemente "un turista che mi ha segnalato una foto".
Tanto l'ho presa da Wikipedia, quindi è sotto licenza Creative Commons. Le mie sono in formato cartaceo, di un'epoca in cui c'era ancora il rullino.
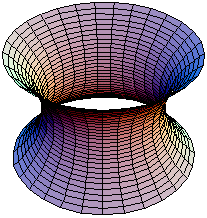
In effetti quello di trovare la superficie di area minima dato un contorno è un problema davvero complesso, tra l'altro il tuo esempio ha un collegamento con l'inizio del discorso del thread: la prima superficie di area minima scoperta è stata la catenoide:DanieleSpace ha scritto: Non è la prima volta che mi trovo di fronte a un caso dove calcoli apparentemente complessi (in questo caso impossibili viste le mancate conoscenze di allora) vengono risolti con un artificio empirico.
Per esempio l'architetto Frei Otto quando progettò lo stadio olimpico di Monaco, creò delle tensostrutture su cui sarebbe stato molto difficile fare i calcoli statici, con in computer ed i software degli anni '60.
Gli venne invece la brillante intuizione di usare delle bolle di sapone e dello spago per creare una sorta di modellino. Se la bolla restava intatta, voleva dire che c'era un certo equilibrio delle tensioni meccaniche, altrimenti doveva rimodellare la struttura.
che minimizza l'area fra le due circonferenze che la delimitano (non è nemmeno immediato accorgersi che un semplice cilindro non è la superficie giusta, per dire la complessità del problema), questa si ottiene ruotando la curva nota come catenaria, che è la curva che descrive una catena appesa alle due estremità. Ebbene, anche se molto simile a una parabola, è proprio la catenaria la curva più adatta a sostenere un ponte, dato che caricata con un peso comporta solo sforzi di compressione. Quindi tutto si ricollega.
Tornando ai nostri egizi, come già detto basta una lampada con un paralume per proiettare un'iperbole su un muro, ma hai presente lo sbattimento di fare quel soffitto solo perchè ti piaceva l'ombra di una lampada? Evidentemente quella forma doveva avere uno scopo più profondo. Ad ogni modo, da quanto abbiamo visto non si può negare che chi ha fatto quel soffitto conoscesse l'iperbole, per il resto non abbiamo nessun elemento concreto per dimostrare che ne conoscesse anche le proprietà matematiche. A meno che non risultasse davvero che il soffitto di roccia della camera coincide esattamente con l'asse dell'iperbole, a quel punto devi quantomeno sapere che un'iperbole ha due rami, cosa che comporta uno studio teorico al livello di quello di Apollonio.
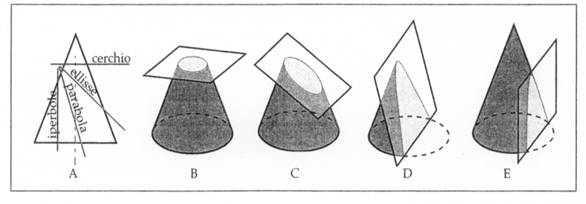
Grazie dell'apporto, non avrei mai immaginato che le curve chiamate "sezioni coniche" fossero sezioni di un cono! Il cono però, a rigore, dovrebbe essere doppio.Fabrizio70 ha scritto: In effetti non servono particolari conoscenze matematiche...
FranZη
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Per quanto ne so, questo fu l'errore che commise Galileo. Anche lui la pensava come te.FranZeta ha scritto: Ebbene, anche se molto simile a una parabola, è proprio la catenaria la curva più adatta a sostenere un ponte, dato che caricata con un peso comporta solo sforzi di compressione.
La catena assume quella forma quando regge solo il suo peso, ma quando la carichi in modo uniforme, assume la forma di una parabola; ovviamente, il peso della catena deve essere trascurabile, rispetto al carico da sostenere.
Per fare un esempio, i cavi di sostegno del Golden Gate sono curvati secondo la parabola y = 1/10 x2 - 0.7
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
Galileo non consceva la catenaria, scoperta solo alla fine del '600, lui sosteneva erroneamente che la catenaria fosse una parabola. Non mi riferivo ai ponti sospesi, ma a quelli in traliccio d'acciaio tipo questo:Rox2 ha scritto: Per quanto ne so, questo fu l'errore che commise Galileo. Anche lui la pensava come te.
Per questo parlavo di sforzi di compressione.
FranZη
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Ti faccio solo notare la contraddizione tra queste due frasi, poi tornerò a Micerino.
Galileo non conosceva la catenaria...
...lui sosteneva erroneamente che la catenaria fosse una parabola.
Tanto per fare un esempio, lo stesso ingegnere del ponte di Garabit (quello che ci hai mostrato), dopo appena 7 anni cambiò idea sulla catenaria e si convertì alla parabola.
Lo dimostra la sua struttura più famosa...
...che si basa sulla funzione y = -0.1278x2 + 0.0111x + 6.1297 ( qui c'è lo studio in formato pdf).
E' chiaro che quei modelli si sono evoluti in in pochissimo tempo, ma nel XIX secolo d.C.; non possiamo applicarli ad una discussione sul soffitto di Micerino.
Potevano andare bene quando li ho citati io come esempi, all'inizio del topic; ma in seguito sei stato tu a dimostrare che abbiamo un'iperbole, quindi non c'entrerebbero comunque né la parabola, né la catenaria.
E come ho già detto io, quel paralume dovrebbe essere parabolico, per proiettare quel fascio di luce sul muro... quindi siamo da capo....come già detto basta una lampada con un paralume per proiettare un'iperbole su un muro
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
- Fabrizio70
-

- Offline
- Senior Member
-

Registered
- Messaggi: 112
- Ringraziamenti ricevuti 8
Il lusso non può mai essere soddisfatto perché, essendo qualcosa di falso, non esiste per esso un contrario vero e reale in grado di soddisfarlo e assorbirlo.
Wilhelm Richard Wagner-1849
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Io ho parlato di "coniche", ovvero curve algebriche del secondo ordine, specificando "tranne la banale circonferenza".Fabrizio70 ha scritto: Prima di fare affermazioni simili hai controllato bene ?
Quelli che ci mostri sono archi molto imprecisi, probabilmente tracciati a mano libera, forse nel tentativo di simulare un semicerchio.
Nulla a che fare con l'iperbole perfetta di Micerino.
Il primo studio serio sulle coniche viene dall'Egitto, perché Apollonio di Perga viveva ad Alessandria.
Perché ci si sarebbe impegnato così, se in quel territorio le conoscevano da oltre 2000 anni?
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
Rox2 ha scritto: Scusami Franz, ma l'ex-moderatore (che ancora vive in me) non mi consente di continuare questo OT.
Ti faccio solo notare la contraddizione tra queste due frasi, poi tornerò a Micerino.
Galileo non conosceva la catenaria...
...lui sosteneva erroneamente che la catenaria fosse una parabola.
Io la chiudo volentieri, basta che sistemiamo le inesattezze. Non c'è nessuna contraddizione: Galileo pensava che la catenaria fosse una parabola, altri matematici decenni dopo hanno stabilito che invece era una curva del tipo y=cosh(x). Lo puoi verificare su qualunque libro di storia della matematica, come pure su wikipedia. Per quanto riguarda la torre Eiffel, ti segnalo che lo "studio" che hai linkato sembra piuttosto un esercizio di un liceale sulle parabole di regressione (fatto maluccio: i punti hanno coordinate intere!), comunque la torre Eiffel non è certo un ponte e quel profilo è una circonferenza:
Ci sono anche studi - seri - sulla forma della torre motivata principalmente dal dover contrastare gli effetti del vento. Quindi non c'è nessuna conversione: solo un altro capolavoro di Gustave Eiffel.
No. Un paraboloide serve a proiettare un fascio (approssimativamente) cilindrico, un paralume come questo:E come ho già detto io, quel paralume dovrebbe essere parabolico, per proiettare quel fascio di luce sul muro... quindi siamo da capo.
...se fosse in metallo invece che vetro, andrebbe benissimo per proiettare un fascio conico dall'apertura in alto. Benissimo nel senso che la curva si vedrebbe, usarlo come guida per scolpire i massi sarebbe un altro paio di maniche...
FranZη
Accedi al sito per partecipare alle discussioni.
- Fabrizio70
-

- Offline
- Senior Member
-

Registered
- Messaggi: 112
- Ringraziamenti ricevuti 8
Io ho parlato di "coniche", ovvero curve algebriche del secondo ordine, specificando "tranne la banale circonferenza".
Quelli che ci mostri sono archi molto imprecisi, probabilmente tracciati a mano libera, forse nel tentativo di simulare un semicerchio.
Nulla a che fare con l'iperbole perfetta di Micerino.
Se questi lavoravano a mano libera e per fortuna si sono ritrovati delle coniche lo stesso ragionamento vale per Micerino...
Il primo studio serio sulle coniche viene dall'Egitto, perché Apollonio di Perga viveva ad Alessandria.
Perché ci si sarebbe impegnato così, se in quel territorio le conoscevano da oltre 2000 anni?
Il fatto che non conosciamo scritti antecedenti non significa nulla , o per caso hai la collezione completa di tutti i libri scritti da Adamo in poi ?
Il lusso non può mai essere soddisfatto perché, essendo qualcosa di falso, non esiste per esso un contrario vero e reale in grado di soddisfarlo e assorbirlo.
Wilhelm Richard Wagner-1849
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Mi hai fatto venire in mente una vecchia barzelletta: "Per tre punti passa una sola retta, purché abbastanza spessa!"
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
- Fabrizio70
-

- Offline
- Senior Member
-

Registered
- Messaggi: 112
- Ringraziamenti ricevuti 8
Mi hai fatto venire in mente una vecchia barzelletta: "Per tre punti passa una sola retta, purché abbastanza spessa!"
Capisco che ammettere di aver scoperto il nulla è difficile però magari con uno sforzo si può fare , ho usato uno spessore maggiore perché le pareti di queste tombe sono affrescate a differenza di Micerino ed è difficile capire l'esatta linea di giunzione ed il metodo di costruzione.
Ritornando alla tua teoria "Quelli che ci mostri sono archi molto imprecisi, probabilmente tracciati a mano libera, forse nel tentativo di simulare un semicerchio." in pratica stai dicendo che una scuola di architettura che per secoli ha costruito monumenti oggi difficilmente replicabili non è in grado di tracciare un semicerchio , questa si che è una barzelletta...
Il lusso non può mai essere soddisfatto perché, essendo qualcosa di falso, non esiste per esso un contrario vero e reale in grado di soddisfarlo e assorbirlo.
Wilhelm Richard Wagner-1849
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Vabbè, speravo di chiuderla con una battuta, ma visto che insisti...Fabrizio70 ha scritto: ho usato uno spessore maggiore perché le pareti di queste tombe sono affrescate a differenza di Micerino ed è difficile capire l'esatta linea di giunzione ed il metodo di costruzione.
Il problema non è lo spessore della linea rossa. E' la malafede con cui cerchi immagini su Google, nel vano tentativo di sputtanare l'interlocutore, facendo le pulci ad ogni parola che scrive.
Quello che non sai è che sono in grado di difendermi, sparando cartucce ben più potenti delle tue. Chi usa l'Argomentum ad hominem è stato per anni il mio bersaglio preferito.
Prima di tutto, usando Geogebra come fai tu, è sufficiente una qualsiasi curvatura per trovarci una conica; basta che ci siano un paio di tratti dove collocare oculatamente i primi quattro punti, poi ci si piazza il quinto in qualche modo, trascinando il mouse fino a dove serve....è difficile capire l'esatta linea di giunzione ed il metodo di costruzione.
...E chissenefrega se il bordo del soffitto sta più fuori che dentro? Tanto la gente non vede più il muro, quando sopra ci piazzi una bella linea rossa che "più o meno" passa da quelle parti.
Il lavoro fatto da FranzEta, sul soffitto di Micerino, è di tutt'altro livello.
La sua sottile iperbole è allineata millimetricamente al bordo del soffitto, in qualsiasi punto della volta:
Tu, invece, non ti sei nemmeno accorto che due immagini su tre, tra quelle che hai mostrato, indicano due pareti opposte della stessa stanza.
Se te fossi reso conto, ti saresti chiesto come mai si ottengono due curve diverse: parabola da una parte ed ellisse dall'altra (pure storta).
Sull'altra immagine, quella di Tutankhamon con il dio Anubi, il taroccamento è anche più interessante.
La prima volta, con una linea spessa due dita, hai mostrato tutta la parete ottenendo un'ellisse:
La seconda volta, "invitato" dalla mia battuta, ti sei sentito costretto ad usare un tratto più sottile; per farlo coincidere, hai dovuto isolare solo la parte alta e ti è uscita un'iperbole...
...sulla stessa parete di prima!!!
A proposito... ti sei dimenticato di ritagliare la foto sui lati destro e sinistro.
Per non infierire, fingo di non aver visto quell'evidente divergenza dopo i punti estremi.
Ma lasciamo stare... Dimentica quello che ho scritto fin qui.
Voglio darti ragione: proviamo a pensare che quei soffitti indichino davvero funzioni coniche.
Una è la tomba più famosa, quella di Tutankhamon, vissuto a metà del XIV secolo a.C.
L'altra è di Sennedjem, un alto funzionario di alcuni decenni più tardi.
Che cosa avremmo dimostrato? Che Micerino conosceva l'iperbole, perché qualcuno l'ha riprodotta 1300 anni dopo?
Come dire che Carlo Magno attraversò i Pirenei con Google Maps.
Non "per secoli", ma per una settantina d'anni....una scuola di architettura che per secoli ha costruito monumenti oggi difficilmente replicabili
Quei "monumenti oggi difficilmente replicabili" non appartengono all'epoca di cui parli tu.
Stai rovesciando tutto nello stesso calderone, tanto sul coperchio ci scriviamo "Antico Egitto" e diciamo che sono sempre loro. In realtà, sai benissimo che sotto quella voce ci stanno 3000 anni di storia.
Quei soffitti curvi, che ci hai mostrato, li saprebbe fare mio figlio con il DAS; tuttavia, 1300 anni prima, quello stesso popolo avrebbe compiuto imprese da fantascienza.
E' questo l'argomento su cui discutere, non se Rox ha scritto una riga sbagliata e farlo passare per idiota.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
- Fabrizio70
-

- Offline
- Senior Member
-

Registered
- Messaggi: 112
- Ringraziamenti ricevuti 8
E' la malafede con cui cerchi immagini su Google, nel vano tentativo di sputtanare l'interlocutore, facendo le pulci ad ogni parola che scrive.
Cioè se io ti faccio una domanda se hai verificato la tua affermazione Non ricordo se l'ho già scritto, ma tranne la banale circonferenza, non si trovano altre coniche in tutto l'Antico Egitto, né ai tempi di Micerino, né durante le 27 dinastie successive. sarebbe fare le pulci sputtanare e malafede ?
Se hai la coda di paglia cambia forum
Tu, invece, non ti sei nemmeno accorto che due immagini su tre, tra quelle che hai mostrato, indicano due pareti opposte della stessa stanza.
Ho preso le prime immagini che ho trovato , mica devo fare una ricerca peer-rewied...
Se te fossi reso conto, ti saresti chiesto come mai si ottengono due curve diverse: parabola da una parte ed ellisse dall'altra (pure storta).
Non mi sono chiesto nulla perché non me ne fotte niente del motivo , sono due coniche ? Si...
Prima di tutto, usando Geogebra come fai tu, è sufficiente una qualsiasi curvatura per trovarci una conica; basta che ci siano un paio di tratti dove collocare oculatamente i primi quattro punti, poi ci si piazza il quinto in qualche modo, trascinando il mouse fino a dove serve.
...E chissenefrega se il bordo del soffitto sta più fuori che dentro? Tanto la gente non vede più il muro, quando sopra ci piazzi una bella linea rossa che "più o meno" passa da quelle parti.
Sull'altra immagine, quella di Tutankhamon con il dio Anubi, il taroccamento è anche più interessante.
La prima volta, con una linea spessa due dita, hai mostrato tutta la parete ottenendo un'ellisse:
La seconda volta, "invitato" dalla mia battuta, ti sei sentito costretto ad usare un tratto più sottile; per farlo coincidere, hai dovuto isolare solo la parte alta e ti è uscita un'iperbole...
...sulla stessa parete di prima!!!
A proposito... ti sei dimenticato di ritagliare la foto sui lati destro e sinistro.
Per non infierire, fingo di non aver visto quell'evidente divergenza dopo i punti estremi.
Bla bla bla ,un sacco di chiacchiere ma ancora non hai indicato DOVE sono i punti sbagliati e perché , che non ti piacciono i risultati è un problema tuo...
Che cosa avremmo dimostrato? Che Micerino conosceva l'iperbole, perché qualcuno l'ha riprodotta 1300 anni dopo?
Sempre 1000 anni prima di Apollonio quindi non torna comunque il tuo ragionamento , se non è studiato non esiste...
Non "per secoli", ma per una settantina d'anni.
Quei "monumenti oggi difficilmente replicabili" non appartengono all'epoca di cui parli tu.
Stai rovesciando tutto nello stesso calderone, tanto sul coperchio ci scriviamo "Antico Egitto" e diciamo che sono sempre loro. In realtà, sai benissimo che sotto quella voce ci stanno 3000 anni di storia.
Sei tu che hai detto forse nel tentativo di simulare un semicerchio. quindi di che epoca stai parlando ?
Preistoria immagino visto che non sono in grado di fare un semicerchio , altro che Antico Egitto...
Quei soffitti curvi, che ci hai mostrato, li saprebbe fare mio figlio con il DAS; tuttavia, 1300 anni prima, quello stesso popolo avrebbe compiuto imprese da fantascienza.
Cioè stai usando un argumentum ab auctoritate qui dentro ? ripassa , sarai più fortunato...
E' questo l'argomento su cui discutere, non se Rox ha scritto una riga sbagliata e farlo passare per idiota.
Se uno risponde che gli antichi egizi non erano in grado di fare un semicerchio è il minimo , per il resto c'è poco da discutere , per fare quella curva non servono conoscenze matematiche particolari
Il lusso non può mai essere soddisfatto perché, essendo qualcosa di falso, non esiste per esso un contrario vero e reale in grado di soddisfarlo e assorbirlo.
Wilhelm Richard Wagner-1849
Accedi al sito per partecipare alle discussioni.
- Fabrizio70
-

- Offline
- Senior Member
-

Registered
- Messaggi: 112
- Ringraziamenti ricevuti 8
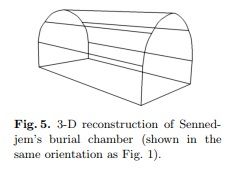
Note that the curvature of the ceiling can be easily determined by simply tracing the contour of one or both end walls. This process can be semi-automated by first selecting a number of points along the contour of each end wall. For each wall, a higher-order polynomial curve is fit to these points, from which a dense sampling of points along each contour can be easily computed. In practice we find given a reasonably dense sampling of points along the contour, as high as a tenth-order polynomial can be used. The final 3-D structure is then determined by directly outputting the shape of the contour in a format readable by a VRML (Virtual Reality Modeling Language) viewer. Shown in
Fig. 5 is a wireframe rendering of the recovered 3-D structure of Sennedjem’s burial chamber. The curvature was determined as described above, and the proportions were determined from published measurements.
Quindi realizzare un iperbole è impossibile , un curva polinomiale di decimo grado è un gioco da ragazzi
Il lusso non può mai essere soddisfatto perché, essendo qualcosa di falso, non esiste per esso un contrario vero e reale in grado di soddisfarlo e assorbirlo.
Wilhelm Richard Wagner-1849
Accedi al sito per partecipare alle discussioni.
- DanieleSpace
-

- Offline
- Senior Member
-

Registered
- Una volta ero certo. Ora sono pieno di dubbi
- Messaggi: 379
- Ringraziamenti ricevuti 65
Eddai, Rox2 ha risposto argomentando per filo e per segno i suoi punti. Non c'è motivo per essere maleducato con lui scrivendo "bla bla bla... non me ne fotte niente".
Se sei in disaccordo, discuti come fa lui, portando spiegazioni, senza aggressività.
Peace and love
Una teoria del complotto è ridicola solo quando sono ridicoli i suoi moventi.
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Rispondo solo a questo, perché su tutto il resto ti sei già infognato a sufficienza da solo.Fabrizio70 ha scritto: Quindi realizzare un iperbole è impossibile , un curva polinomiale di decimo grado è un gioco da ragazzi
Tuttavia, per chi non ha competenze di matematica, questa tua ultima frase può trarre in inganno.
La risposta è SI'!
La curva di decimo grado ti esce fuori a casaccio, mentre la conica devi progettarla apposta.
Se prendi una matita e tracci una curva sul muro, a mano libera, quella è comunque una funzione matematica.
Forse ci vorrà un intera lavagna, per scrivere tutta l'equazione... ma qualsiasi curva, comunque complessa, è matematicamente individuabile su due assi cartesiani, compreso lo scarabocchio di un bambino dell'asilo.
Tuttavia è quasi impossibile che sia un'iperbole, oppure una parabola. Se lo fosse, si tratterebbe di un caso eccezionale come il cerchio di Giotto.
Per chi ancora non avesse capito, faccio un esempio molto semplice.
Se prendo quattro stecchini e li appoggio sul tavolo, punta contro punta, sono sicuro di aver disegnato un rombo; comunque li abbia disposti.
Se invece voglio ottenere un quadrato, devo farlo apposta.
Pertanto, se la tomba di Sennedjem richiede una funzione di decimo grado, questa è una dimostrazione evidente che l'hanno tracciata a mano.
...E anche in modo impreciso, perché su pareti opposte ci sono due curve diverse; lo hai dimostrato tu nei tuoi post precedenti.
Inoltre, anche senza Geogebra, il tracciamento a mano libera si vede a occhio, grazie agli animali dipinti sotto l'arco che fanno da riferimento.
I due cinocefali sembrano padre e figlio, tanto sono diversi nelle dimensioni, per farli entrare nello spazio lasciato dalla curvatura:
Dall'altra parte, con i due sciacalli si vede un po' meno, ma ci sono i gli occhi di Ra a manifestare l'evidente imprecisione.
Approfitto per riproporre la domanda in modo diverso.
- Nel 2600 a.C., lavorando il granito, gli operai di quel popolo tracciano un'iperbole millimetricamente perfetta. Inoltre la riproducono sempre uguale su 18 blocchi adiacenti, tutti dello stesso durissimo materiale.
- Oltre 1000 anni più tardi, con tutti gli sviluppi della metallurgia, della matematica, della meccanica, provano a tracciare una curvatura sulla tenera roccia calcarea; come risultato, ottengono una deformazione che si vede a occhio nudo, palesemente differente su pareti opposte, così irregolare da richiedere una funzione di decimo grado per essere definita matematicamente.
Come è possibile?
Io ce l'avrei, una mezza idea... Tu ce l'hai?
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
FranZη
Accedi al sito per partecipare alle discussioni.
- Fabrizio70
-

- Offline
- Senior Member
-

Registered
- Messaggi: 112
- Ringraziamenti ricevuti 8
Se sei in disaccordo, discuti come fa lui, portando spiegazioni, senza aggressività.
Quindi secondo te dire che manipolo i dati per avere ragione è discutere senza aggressività....
Con il tuo metodo diventa conica pure la mia lavastoviglie.
Mi hai fatto venire in mente una vecchia barzelletta: "Per tre punti passa una sola retta, purché abbastanza spessa!"
Ne deve passare di acqua sotto i ponti prima che qualcuno si possa permettere di darmi del cazzaro...
Il lusso non può mai essere soddisfatto perché, essendo qualcosa di falso, non esiste per esso un contrario vero e reale in grado di soddisfarlo e assorbirlo.
Wilhelm Richard Wagner-1849
Accedi al sito per partecipare alle discussioni.
- Fabrizio70
-

- Offline
- Senior Member
-

Registered
- Messaggi: 112
- Ringraziamenti ricevuti 8
La curva di decimo grado ti esce fuori a casaccio, mentre la conica devi progettarla apposta.
.........
Tuttavia è quasi impossibile che sia un'iperbole, oppure una parabola. Se lo fosse, si tratterebbe di un caso eccezionale come il cerchio di Giotto.
La seconda volta, "invitato" dalla mia battuta, ti sei sentito costretto ad usare un tratto più sottile; per farlo coincidere, hai dovuto isolare solo la parte alta e ti è uscita un'iperbole...
Veramente di iperboli ne sono uscite tre , tutti Giotto a quanto pare , che poi a differenza di Micerino il resto delle pareti siano curve è un altro discorso che tu usi per dire che le curve non sono coniche ma per quel tratto SONO iperboliche , lo hai detto tu stesso.
Inoltre, anche senza Geogebra, il tracciamento a mano libera si vede a occhio, grazie agli animali dipinti sotto l'arco che fanno da riferimento.
Scusa ma io dell'occhio nudo non mi sono mai fidato , hai qualche contestazione da fare sul posizionamento dei punti o per buona parte del soffitto è presente un iperbole ?
Come è possibile?
Io ce l'avrei, una mezza idea... Tu ce l'hai?
Se hai una idea tirala fuori , non ho tempo da perdere con gli indovinelli...
Il lusso non può mai essere soddisfatto perché, essendo qualcosa di falso, non esiste per esso un contrario vero e reale in grado di soddisfarlo e assorbirlo.
Wilhelm Richard Wagner-1849
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Anch'io!... Anch'io!Fabrizio70 ha scritto: Veramente di iperboli ne sono uscite tre , tutti Giotto a quanto pare
Oggi mi sono divertito un po' con Geogebra.
Prima sono andato sul Paint di Windows, per tracciare un arco con una strisciata del mouse:
Chissà che non sia una conica?
Magari... con un po' di tolleranza... Proviamoci!
Et voilà! Ecco servita una splendida ellisse!
Chissenefrega se diverge sugli estremi? Tanto poi la ritaglio e la mostro come mi pare...
Anzi, se sul forum qualcuno scopre il trucco... Sai che faccio?
Gli mostro la curva già ritagliata, in modo da isolare la parte più regolare.
A questo punto cerco la conica, così dovrebbe venirmi anche meglio.
Risultato perfetto!... Anch'io come Giotto!!!
Speriamo non si accorga nessuno che prima era un'ellisse, mentre adesso è diventata un'iperbole...
Adesso torniamo seri. Mi sembra già di sentire la domanda:
- Ma scusa eh... se quel giochino si può fare con qualsiasi curva, non vale anche per il soffitto di Micerino?
La risposta è NO!!!
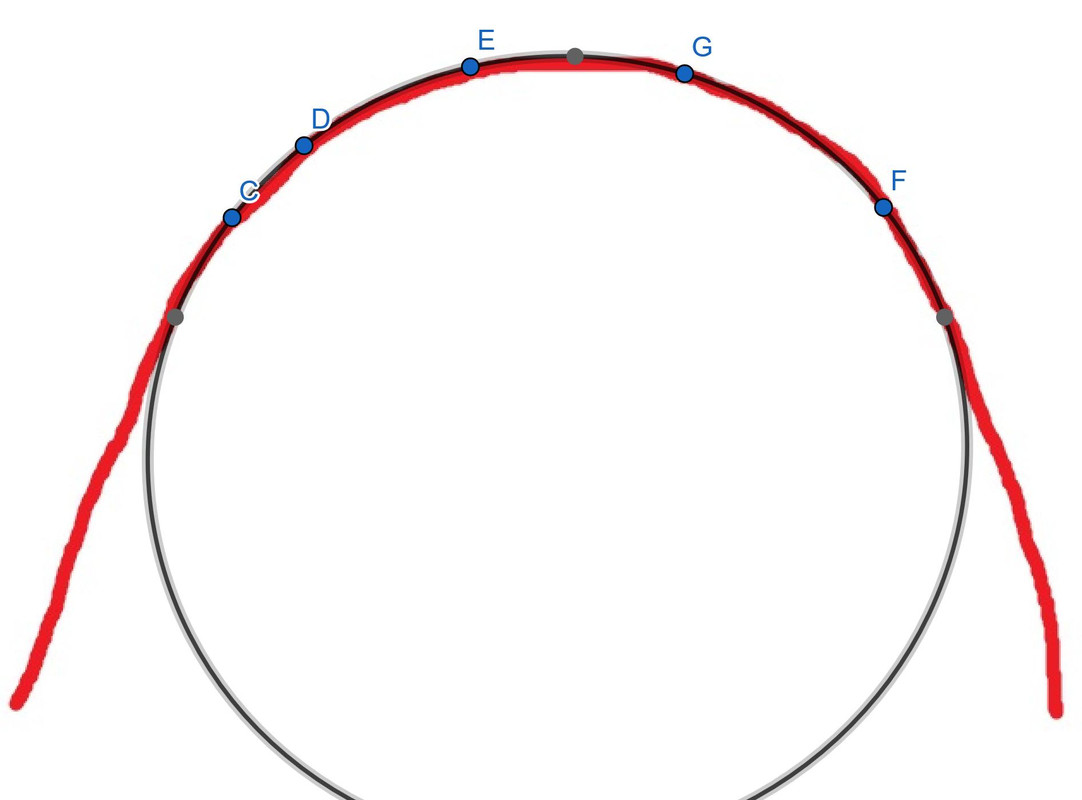
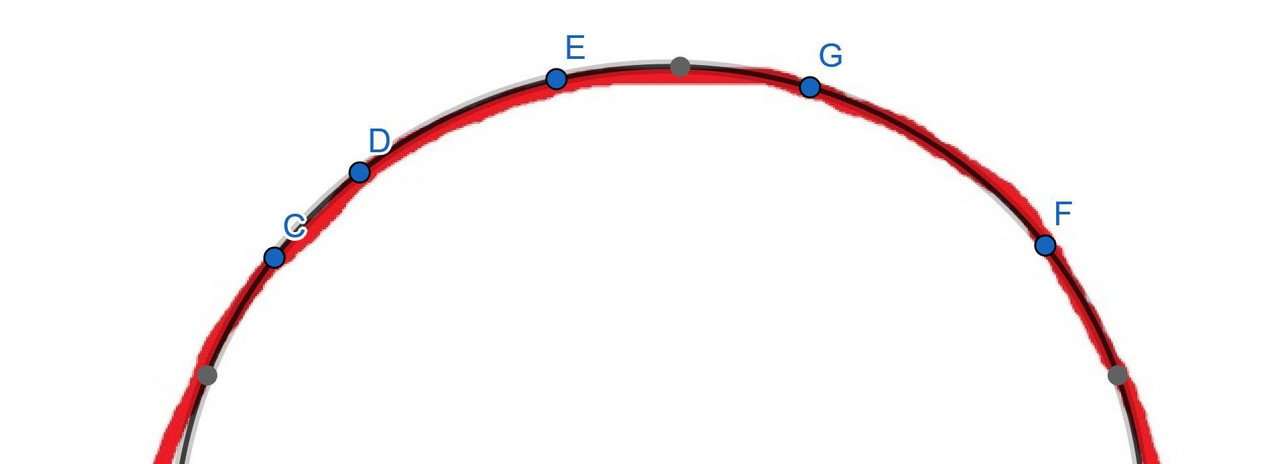
La differenza risulta evidente analizzando il lavoro di FranzEta, che ripropongo di nuovo:
- Innanzitutto, ha operato sull'immagine che gli ho segnalato io, nonostante la posizione decentrata del fotografo (che ha spiegato essere trascurabile). Non è andato a cercare con Google una foto che facesse al caso suo.
- In seguito, per ottenere la massima precisione, si è fatto addirittura un ingrandimento, ma senza ritagliare nulla di significativo.
- Poi ha selezionato l'intera curva, su una lunghezza di quasi tre metri, impostando i primi due punti in corrispondenza degli spigoli. Non ha isolato il tratto che gli faceva comodo.
- Infine, ha ottenuto un'iperbole che si adatta al soffitto in modo precisissimo, malgrado il tratto sottile; le tolleranze sono invisibili ad occhio nudo, in ogni singolo millimetro di quei tre metri, mentre il fuoco è esattamente in verticale sotto il vertice.
Conclusione.
La tomba di Sennedjem la so disegnare pure io, strisciando un pezzo di carbonella su un muro bianco.
Con il soffitto di Micerino... mi rimane un tantino più difficile.
D'accordo, comincio io...Fabrizio70 ha scritto: Se hai una idea tirala fuori , non ho tempo da perdere con gli indovinelli...
Quel soffitto non lo ha fatto Micerino!
E' opera di qualcuno che sapeva maneggiare il granito con facilità, ma soprattutto, che sapeva tagliarlo a forma di iperbole con precisione chirurgica.
In questa sede, non ha importanza se erano gli Atlantidei, gli extraterresti, i giganti, gli stregoni o i Rettiliani; ci sono ipotesi più realistiche o più fantasiose; ognuno si scelga quella che gli pare (magari aprendo un nuovo topic).
Quello che appare certo è che i faraoni hanno trovato tutto già lì: Sfinge, piramidi e relativi templi, tutto costruito da altri in epoche precedenti.
Il povero Sennedjem, invece, ha dovuto farsi fare il soffitto con i mezzi che aveva.
Devo dire che gli è venuto anche bene, con le tecnologie dell'epoca.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
Rox2 ha scritto: La differenza risulta evidente analizzando il lavoro di FranzEta, che ripropongo di nuovo
In effetti come puoi constatare dall'ordine alfabetico dei punti scelti, sono partito dai due spigoli, poi ho aggiunto il vertice e infine per ultimi due punti all'incirca equidistanti da questi, per non lasciare nulla alla soggettività nella scelta dei punti (e anche per un discorso di precisione). Detto questo, nei post precedenti non ho specificato una cosa che forse giocherellando con Geogebra potresti verificare tu stesso. In effetti è praticamente impossibile ottenere una parabola tramite "conica per cinque punti", perchè la parabola è un caso limite fra le coniche e sono sufficienti 4 punti per individuarla. Insomma, per ottenere una parabola devi avere qualcosa di davvero ma davvero parabolico!
Però, pur nell'approssimazione che si ha posizionando i punti, se ci trovassimo davanti a una curva molto simile ad una parabola, ci dovremmo aspettare di trovare con Geogebra o un'ellisse molto allungata o un'iperbole con due rami molto distanti, cosa che non accade con il soffitto di Micerino. In più, e questo l'ho già segnalato, se il soffitto è con ottima approssimazione iperbolico, beh allora non può anche essere parabolico con approssimazione altrettanto buona.
FranZη
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Nel mio post precedente ho fatto il "cattivo esempio", proprio perché appaia macroscopica la professionalità del tuo operato, per quanto semplice e rapido possa essere stato per te.FranZeta ha scritto: ...se il soffitto è con ottima approssimazione iperbolico, beh allora non può anche essere parabolico con approssimazione altrettanto buona.
Ho proposto volutamente quei disegnini infantili, sul Paint di Windows. Volevo mostrare la differenza, tra chi usa Geogebra per gioco e chi ne è un professionista.
Nel lavoro che hai fatto, e di questo mi ero dimenticato, ti sei preso la briga di mostrarci ANCHE la parabola, in corrispondenza dello stesso fuoco, disegnandola perfino con un colore diverso a beneficio di chi ti legge.
Non basta avere la chitarra per essere un chitarrista.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
- DanieleSpace
-

- Offline
- Senior Member
-

Registered
- Una volta ero certo. Ora sono pieno di dubbi
- Messaggi: 379
- Ringraziamenti ricevuti 65
- Se lanci un sasso diagonalmente verso l'alto, la traiettoria che descrivi è una parabola.
- Se guardi una gara di salto con l'asta, l'attrezzo caricato si piega a parabola.
- Se tieni una cordicella alle due estremità, tenendola allentata, quando la carichi con 10 pesi uguali alla stessa distanza tra loro, assume la forma di una parabola.
Mi fermo qui... E' solo per capire che ci sono diversi modi, con mezzi primitivi, per ottenere una parabola.
Tuttavia, non ne conosco nemmeno uno, per formare un'iperbole.
Non sono certo abile in matematica ma mi sono scervellato per ore a cercare di trovare un metodo con corde e cordini cui fosse legato uno scalpello, onde poter scolpire un arco iperbolico. Inutile dire che ho fallito miseramente
Poi però ho trovato questa foto:
Copia della didascalia: Everyday examples of projective geometry:a circular lampshade casts a hyperbolic shadow (photos taken by Doris Schattschneider).
Viene da un sito subordinato a quello dell'università di York (UK) , facoltà di matematica e statistica.
Loro dicono che è un fascio di luce iperbolico (non parabolico).
Non voglio togliere nulla alla vostra dissertazione, ma prima di parlare di "antichi popoli" o di quelli che c'erano "prima", alla LUCE di questo materiale, ribadisco la domanda, ora formulata in modo più preciso.
È possibile che il povero scalpellino addetto al famoso soffitto, abbia scolpito l'iperbole, semplicemente seguendo la luce proiettata dalla sua lampada ad olio, pur non capendo una mazza di matematica ?
Una teoria del complotto è ridicola solo quando sono ridicoli i suoi moventi.
Accedi al sito per partecipare alle discussioni.
- Fabrizio70
-

- Offline
- Senior Member
-

Registered
- Messaggi: 112
- Ringraziamenti ricevuti 8
Risultato perfetto!... Anch'io come Giotto!!!
No tu hai barato , prima hai disegnato la curva con strumenti matematici e poi hai ripassato sopra con paint , vedi com'è facile dare del cazzaro senza prove ?
Non è andato a cercare con Google una foto che facesse al caso suo.
Ho cercato foto con soffitti curvi , il caso l'hai creato tu...
Poi ha selezionato l'intera curva, su una lunghezza di quasi tre metri, impostando i primi due punti in corrispondenza degli spigoli. Non ha isolato il tratto che gli faceva comodo.
Tanto per cominciare non hai notato la piccola differenza che una tomba ha le pareti verticali , l'altra ha le pareti curve quindi gli spigoli è difficile trovarli , la parte che mi "fa comodo" è oltre il 70% della volta non di certo il pezzettino che hai isolato te...
Del resto per te quello è un tentativo di simulare un semicerchio , come uno possa vederci un semicerchio è un mistero che rimane negli annali...
Quello che appare certo è che i faraoni hanno trovato tutto già lì: Sfinge, piramidi e relativi templi, tutto costruito da altri in epoche precedenti.
Il povero Sennedjem, invece, ha dovuto farsi fare il soffitto con i mezzi che aveva.
Devo dire che gli è venuto anche bene, con le tecnologie dell'epoca.
Tutto questo casino è nato perché pensavo di ragionare con una persona seria ed in buonafede , evidentemente mi sbagliavo , le immagini che ho trovato non sono quelle "che mi fanno comodo" , sono le prime che ho trovato che ad occhio erano soffitti con curve coniche ( a differenza tua che ci vedi i semicerchi ) , vista la tua malafede ho approfondito le ricerche...
Opssss, la tomba del figlio di Micerino , Shepseskaf , a differenza del padre si è fatto costruire una mastaba a Saqqara , e fin qui ci potrebbe stare che gli stessi Atlantidei, gli extraterresti, i giganti, gli stregoni o i Rettiliani che hanno costruito la tomba al padre hanno fatto un favore al figlio ma.....
con la tomba di Mentuhotep III costruita 500 anni dopo a Deir el-Bahari vicino a Luxor i conti non tornano proprio , come già ti avevo detto stiamo parlando di aria fritta , quindi la prossima volta che uno ti domanda Prima di fare affermazioni simili hai controllato bene ? metti da parte l'orgoglio e rispondi con un semplice NO , oltre a fare una figura migliore eviti di passare da visionario ( i semicerchi...)
P.S:
Quando ci provai io, l'egittologo che ci faceva da guida mi prese per il culo tutto il pomeriggio.
Riuscì a farlo smettere dicendogli, davanti a tutti: "Provaci tu, a scavare due metri cubi con attrezzi di rame, da un parallelepipedo di granito; quando hai finito chiamami, che ti offro da bere."
A quanto vedo sei abituato con i fessacchiotti...
Questa è pure più dura del granito , ed é solo una delle tante statue in granito che oggi sono in giro per il mondo oltre che in Egitto , pure qui i faraoni se le sono trovate già fatte?
Il lusso non può mai essere soddisfatto perché, essendo qualcosa di falso, non esiste per esso un contrario vero e reale in grado di soddisfarlo e assorbirlo.
Wilhelm Richard Wagner-1849
Accedi al sito per partecipare alle discussioni.
- DanieleSpace
-

- Offline
- Senior Member
-

Registered
- Una volta ero certo. Ora sono pieno di dubbi
- Messaggi: 379
- Ringraziamenti ricevuti 65
ho preso una normale candelina, un cero tipo quelli da chiesa e l'ho messo in un bicchiere cilindrico opaco.
Poi ho messo il tutto per terra, a ridosso del muro del soggiorno.
Ho ottenuto quanto segue:
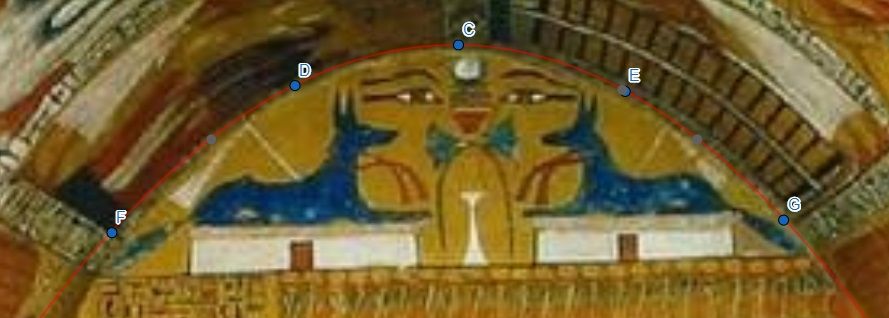
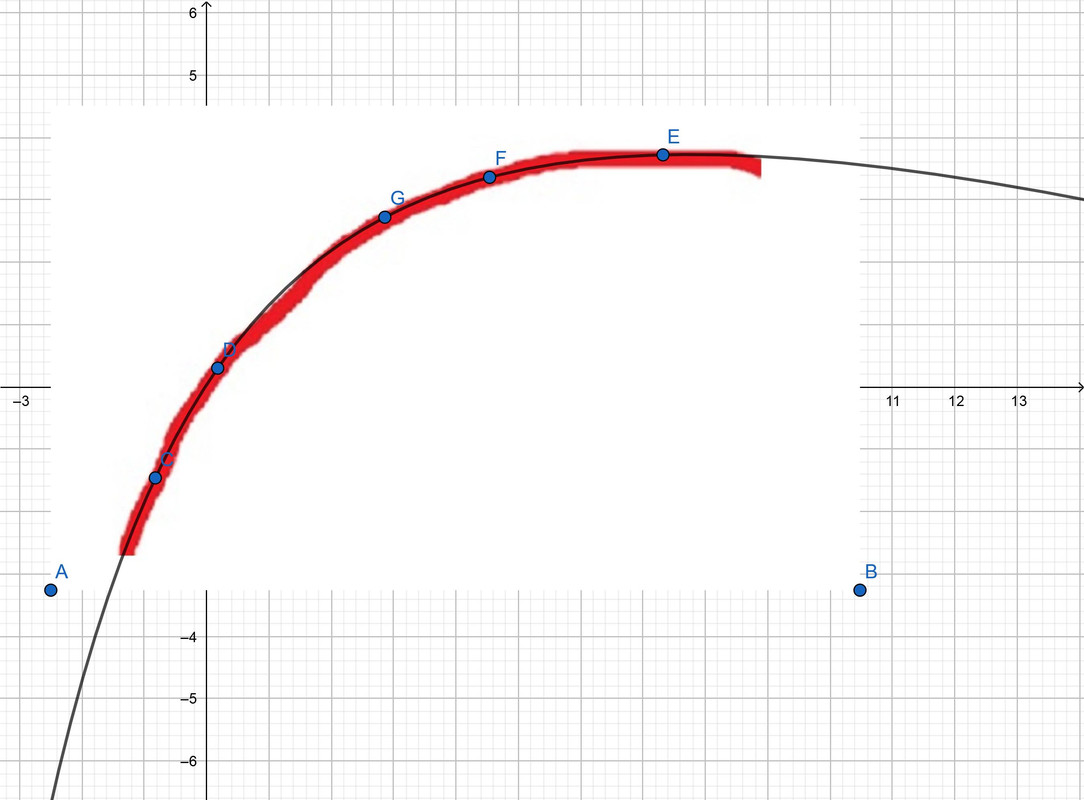
Poi ho messo tutto in Geogebra, il tool che mi avete fatto scoprire voi in questo thread e ho selezionato 5 dei 6 punti che ho tracciato (C, D, E, F, G), seguendo la luce sul muro.
Immediatamente mi ha creato una conica iperbolica che a me, sembra passare esattamente sulla curva di luce proiettata dalla candela.
Il punto H non fa parte del calcolo della curva ma coincide perfettamente.
Rimane ora il problema pratico che l'iperbole è ribaltata rispetto al soffitto da scolpire, ma questo è un ostacolo facilmente superabile, intanto abbiamo il segreto dell'iperbole.
Una teoria del complotto è ridicola solo quando sono ridicoli i suoi moventi.
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Vedi, Fabrizio... se io fossi come te, mi basterebbe questa tua frase per ignorare tutto quello che scrivi. Potrei facilmente appellarmi all'Argumentum ad hominem, facendoti passare per idiota e togliendo importanza anche agli altri tuoi argomenti.Fabrizio70 ha scritto: No tu hai barato , prima hai disegnato la curva con strumenti matematici e poi hai ripassato sopra con paint...
Ma io non sono così.
Ti risponderò punto per punto, su Shepseskaf, su Mentuhotep II (non III, immagino sia un errore di battitura), e anche su Ramesse II.
Ma proprio perché intendo discuterne nel merito, senza cercare di sputtanare nessuno, lo farò in messaggi separati che ora non ho tempo di scrivere.
Per adesso, ti invito a guardare le cose da un altro punto di vista.
Forse (e sottolineo forse) tu credi che io sia qui per vantarmi, per apparire come "quello che ha trovato la conica di Micerino, importantissima scoperta archeologica che cambierà il Mondo...", invece non me ne frega un cazzo.
Ho già scritto a Franz che se vuole contattare qualche rivista può farlo lui, definendomi semplicemente "un turista".
Il mio scopo te l'ho già indicato due messaggi fa: ho delle convinzioni che riguardano l'Antico Regno, da circa 30 anni, ma le mie idee sono in contrasto con la versione ufficiale dei libri di Storia.
Sono qui per parlarne, perché LuogoComune ha sempre dimostrato una certa apertura, verso ipotesi non convenzionali.
Visto che le ho già esposte, prova a riguardare le tue segnalazioni su Shepseskaf, Mentuhotep e Ramesse, prima che ne parli io.
Forse ti accorgerai che stai dando un grosso contributo alle mie idee "eretiche", non posso che ringraziarti.
Se non lo capisci da solo, significa che il tuo scopo è quello che io sospetto dall'inizio: fare le pulci ad ogni singola frase di Rox, nel tentativo di sputtanarlo in qualche modo.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Non avevo capito che l'avessi interpretato come "orgoglio". Anzi, avevo dato per scontato che NESSUNO conosce TUTTE le tombe ed i templi dell'Egitto.Fabrizio70 ha scritto: Prima di fare affermazioni simili hai controllato bene ? metti da parte l'orgoglio e rispondi con un semplice NO
La mia frase si riferiva alle opere che conosco io, perché ne ho letto o perché le ho viste di persona; visto che sono parecchie, credo di potermelo permettere.
Se il tuo scopo era questo, direi che possiamo finirla qui. Non ho mai avuto alcuna intenzione di passare per "insigne professore di Egittologia", anzi, non me ne frega una cippa.
Ora passerei alle foto che ci hai segnalato, cominciando dal'inizio...
Quando andai a Saqqara, la guida ci mostrò solo la piramide di Zoser, perché era l'unica aperta ai turisti. Di conseguenza, non ho mai visto la camera sepolcrale di Shepseskaf ed il suo soffitto.
Inoltre, si tratta di un faraone poco conosciuto e dal regno molto breve; sui miei libri se ne parla, ogni tanto, ma tra le immagini non c'è quel soffitto. Anche tu, devi aver faticato parecchio a trovare quell'immagine.
Comuque, è abbastanza evidente che quella tomba è stata costruita in due tempi, forse tre.
Gli ambienti sotterranei mostrano abilità costruttive molto superiori, rispetto alla parte esterna; questo lo sapevo da molto prima che tu mi mostrassi il soffitto iperbolico, che adesso mi appare come un'ulteriore conferma.
In pratica, è come se Shepseskaf avesse trovato quei vani bell'e pronti: stanze, corridoi e cunicoli, per poi appropriarsene facendoci erigere sopra la sua mastaba.
Questo è l'aspetto esterno:
Blocchi di pietra calcarea da circa una tonnellata, talvolta meno, tra i quali è possibile infilare una mano.
Ora andiamo dentro:
Fino alla stanza dell'iperbole:
In tutto, ci sono oltre 200 blocchi di granito, tra le 5 e le 15 tonnellate, così perfettamente squadrati che non ci passa la lama di un taglierino.
Secondo l'archeologia ufficiale, la scusa è sempre quella: il Faraone è morto prima di finire l'opera, quindi hanno dovuto completarla in fretta.
E' una palese barzelletta, ma quando non hai di meglio...
Sì... lo so...
E che rivestimento! Lo vediamo bene su quella di Snefru, dove è ancora rimasto:
Blocchi tagliati alla perfezione, ancora lisci dopo millenni di erosione atmosferica.
Anche la piramide di Micerino sarebbe stata costruita in due tempi. E la scusa è sempre la stessa.
Un po' come quella dei tombaroli, buona per tutte le stagioni.
Alla prossima, parliamo di Mentuhotep...
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
E' sempre interessante e istruttivo vedere una verifica empirica di una affermazione teorica, e il tuo esperimento con la candela verifica quanto già ribadito più volte. Credo di aver già risposto qui alla tua domanda:DanieleSpace ha scritto: Non voglio togliere nulla alla vostra dissertazione, ma prima di parlare di "antichi popoli" o di quelli che c'erano "prima", alla LUCE di questo materiale, ribadisco la domanda, ora formulata in modo più preciso.
È possibile che il povero scalpellino addetto al famoso soffitto, abbia scolpito l'iperbole, semplicemente seguendo la luce proiettata dalla sua lampada ad olio, pur non capendo una mazza di matematica ?
Tornando ai nostri egizi, come già detto basta una lampada con un paralume per proiettare un'iperbole su un muro, ma hai presente lo sbattimento di fare quel soffitto solo perchè ti piaceva l'ombra di una lampada? Evidentemente quella forma doveva avere uno scopo più profondo. Ad ogni modo, da quanto abbiamo visto non si può negare che chi ha fatto quel soffitto conoscesse l'iperbole, per il resto non abbiamo nessun elemento concreto per dimostrare che ne conoscesse anche le proprietà matematiche. A meno che non risultasse davvero che il soffitto di roccia della camera coincide esattamente con l'asse dell'iperbole, a quel punto devi quantomeno sapere che un'iperbole ha due rami, cosa che comporta uno studio teorico al livello di quello di Apollonio.
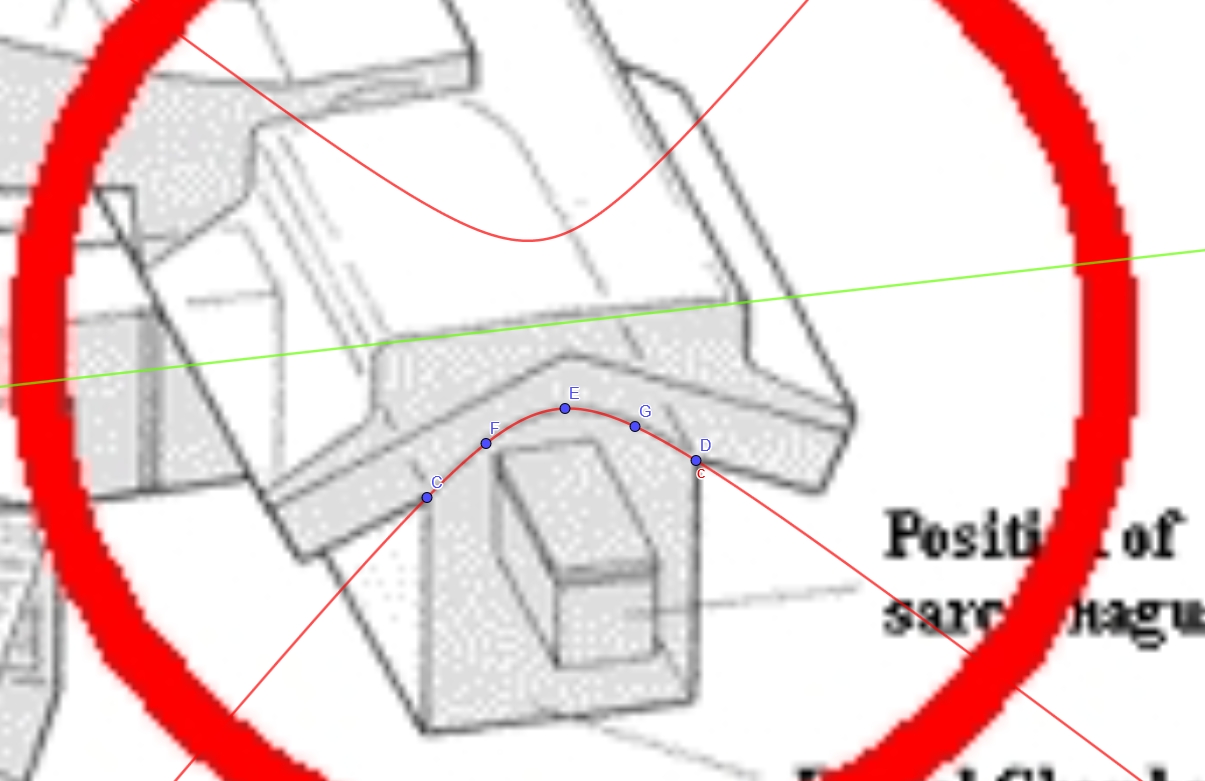
Riassumendo: proiettare un'iperbole su un muro è cosa assai semplice, usare questo metodo per ricavare il soffitto di Micerino è invece impresa assai ardua, non certo per il fatto che l'iperbole risulta rovesciata (anzi, questo se mai è un vantaggio dato che è ragionevole pensare che i blocchi siano stati scolpiti prima di essere messi in opera). L'ombra del lume fornirebbe una guida per un profilo*, questo andrebbe replicato su ogni masso che compone il soffitto per tutta la profondità del masso, inutile dire che spostando la lampada cambia l'iperbole proiettata**. Direi che è un lavoraccio assurdo e assolutamente insensato a meno che quella particolare forma non avesse un significato molto più profondo dell'ombra di una candela. Insomma, pensare che tutto si risolva così è come ipotizzare che la piramide di Cheope abbia quelle proporzioni per caso, o perchè così risultava graziosa.
*Riporto nuovamente uno schema della camera per capire dicosa si sta parlando:
**Diciamo che, sempre nell'ottica dell'iperbole ricavata come ombra, un'ipotesi più convincente sarebbe che abbiano dapprima usato quest'ombra per costruire un profilo di riferimento, intagliando un'asse di legno per esempio, e poi preso questa come guida per scolpire i massi. Ma intagliare un'asse di legno (o altro strumento simile) in forma iperbolica significa conoscere l'iperbole come curva, poi come già detto questo non è sufficiente a dimostrarne eventuali conoscenze matematiche.
FranZη
Accedi al sito per partecipare alle discussioni.
- CharlieMike
-

- Offline
- Platinum Member
-

Registered
- Messaggi: 2950
- Ringraziamenti ricevuti 435
Volevo dire la mia.
Io non sono competente in nessuna di queste materie, ma personalmente non direi che gli antichi non avessero determinate conoscenze, dato che sparse per il mondo ci sono moltissime costruzioni di cui non si riesce a spiegare come siano state realizzate con i mezzi disponibili all'epoca, e che alcune risultano impossibili da replicare anche con i nostri mezzi moderni.
Ma non voglio addentrarmi oltre in una discussione che non posso sostenere, per cui continuerò a leggervi.
Ho solo una domanda da porvi.
Così come le api hanno scelto l'esagono come forma più ergonomica per la realizzazione delle celle nel loro alveare, qual è la forma in natura più utilizzata per sorreggere una volta o un arco?
Accedi al sito per partecipare alle discussioni.
- Messaggi: 106
- Ringraziamenti ricevuti 51
Vorrei cominciare da questa frase di Franz...
Sarebbe "assurdo ed insensato" se considerassimo solo le dimensioni dei blocchi ed il loro numero; ma diventa impossibile se parliamo anche di materiali e peso.FranZeta ha scritto: Direi che è un lavoraccio assurdo e assolutamente insensato a meno che quella particolare forma non avesse un significato molto più profondo dell'ombra di una candela.
Cominciamo dal materiale: il granito.
Quando DanieleSpace parla di "scalpellini", fa pensare ad un operaio con cesello, sgorbia o altro attrezzo in acciaio; Micerino, invece, è vissuto 700 anni prima che gli Egizi scoprissero il bronzo, più altri 700 per arrivare al ferro.
Inoltre, non c'è solo l'iperbole.
In qualsiasi parte della stanza, comprese le pareti verticali, non c'è un solo punto in cui si riesca ad infilare un capello tra due blocchi.
Ora passiamo al peso.
Quei 18 blocchi del soffitto pesano oltre 800 kg ciascuno e stanno ad oltre 3 metri di altezza, in una stanza larga 2 metri e mezzo.
Non è che ci puoi mettere 40 persone, lì dentro, per tirarlo su.
Ma anche se fosse possibile, guardate il blocco su cui è fissata la telecamera...
Quello pesa oltre 2 tonnellate.
Infine, tutti quei blocchi dovevano passare da qui...
...perché siamo 15 metri sotto la superficie ed altri passaggi non ce ne sono.
Quanti operai ci potevano entrare, tra quelli dietro il blocco e quelli davanti?
Scherzi?...charliemike ha scritto: Scusate l'intromissione.
Volevo dire la mia.
Siamo qui per questo!
Questo rende la tua opinione anche più interessante, visto come si comportano gli archeologi "competenti".Io non sono competente in nessuna di queste materie
Esatto... ma dipende da quanto antichi.non direi che gli antichi non avessero determinate conoscenze
Da come si presentano le cose, sembrerebbe che i "molto antichi" avessero conoscenze ingegneristiche da urlo, decisamente superiori a chi progetta i ponti di Genova.
Quelli "un po' meno antichi", al contrario, avevano esattamente le abilità che ci si aspetta, dalla loro epoca.
Sì, infatti... Si chiamano "OOPArt", che significa "Out Of Place ARTifacts" ovvero "Manufatti fuori luogo".sparse per il mondo ci sono moltissime costruzioni di cui non si riesce a spiegare come siano state realizzate
Qui non intendo parlarne, per i motivi che ho spiegato all'inizio.
Esiste un altro topic dove hanno cercato di organizzare un elenco. Io non intendo ignorare gli altri, ma preferisco che ognuno venga discusso con la visibilità che merita, in un topic tutto suo.
Ho cominciato con Micerino perché non se ne parla mai, poveraccio...
Non mi intendo di Geologia, ma non credo che in natura esistano archi...qual è la forma in natura più utilizzata per sorreggere una volta o un arco?
La caverne naturali hanno una forma casuale, legata ad erosione, frane o ad altri fenomeni geologici.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Accedi al sito per partecipare alle discussioni.
- DanieleSpace
-

- Offline
- Senior Member
-

Registered
- Una volta ero certo. Ora sono pieno di dubbi
- Messaggi: 379
- Ringraziamenti ricevuti 65
Hai ragione, più che altro rispondevo a Rox 2 che diceva di non conoscere esempi di iperbole in natura. Non ne conoscevo nemmeno io, fino all'altro giorno.
Ricordo che avevi menzionato la lampada col paralume ma non riuscivo ad immaginare come quella lampada potesse proiettare un'iperbole. Nella mia testa mancava l'immagine della luce proiettata da quel tipo di lampada.
Ancora adesso, non sono convinto che la lampada (della tua foto), con paralume in vetro possa proiettare una iperbole.
Da quel che ho capito serve una sorgente di luce puntiforme e un cerchio ( o cilindro) opaco.
Inoltre, non credo che all'epoca delle piramidi, fossero in grado di usare il vetro per le lampade ;o)
La dimostrazione matematica dovrebbe essere fattibile, del tipo..."Dato il punto fisso ed il cerchio perpendicolare alla superficie del muro... Dimostrare che le rette passanti per il punto che attraversano il cerchio e che intersecano il piano del muro...disegnano un'iperbole"
Ma non vorrei dire eresie, non è il mio campo :o)
@Rox2
Hai ragione anche tu... stupidamente non avevo pensato che non conoscessero ancora il ferro o il bronzo
Io non ho idea di come abbiano fatto a scolpire quelle pietre. Un lavoro mostruoso.
Mi dispiace anche di aver un po' demistificato la tua / vostra scoperta che rimane comunque eccezionale. Inoltre non è detto che abbiano usato il metodo della lampada.
Forse è il primo manufatto della storia ad avere quella forma, se ho capito bene.
Riguardo al tema, sarebbe logico pensare che abbiano fatto delle "prove" prima di riuscire a scolpire le pietre con quel profilo.
QUalcuno sa se abbiano ritrovato pietre con profilo simile, disseminate qua e là ? Immagino di no.
Una teoria del complotto è ridicola solo quando sono ridicoli i suoi moventi.
Accedi al sito per partecipare alle discussioni.