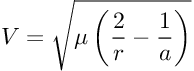- Messaggi: 746
- Ringraziamenti ricevuti 263
-
-

- Quando lo scettico...
- Ciao a tutti: grazie ad Azrael per aver condiviso la sua interessante esperienza. Azrael credo che lavori...
- da Davide71
- 26/04/2024 11:16
-
-
-

- L'angolo dei Meme
- da Nomit
- 24/04/2024 17:07
-
-
-

- LA GRAN TARTARIA E...
- Sono messaggi simbolici/massonici. Esattamente come l'inchino della Concordia al giglio (vedasi loggia...
- da marlo
- 23/04/2024 18:36
-
-
-

- Cosa state ascolta...
- Lasciamoci andare, a naufragare nel NON tempo. Coraggio che il meglio è passato......
- da Volano49
- 20/04/2024 21:02
-
Quanta energia serviva per andare sulla luna?
Accedi al sito per partecipare alle discussioni.
Riguardo alla Sua interessante inchiesta sulle missioni lunari Apollo, ma in generale per tutte quelle millantate come tali anche da altri Paesi (Russia molto tempo fa, Cina e India recentemente), per non parlare delle sonde mandate sugli altri pianeti, dobbiamo constatare che prendersi gioco dei più piccoli con menzogne colossali ha infettato un po’ tutte le elite di questo mondo, dall’amministrazione Kennedy in poi. Ciò paga generalmente in termini di consenso e fondi pubblici erogati sotto falso nome, quindi i potenti se ne lasciano facilmente contagiare. Poi rispondono paternamente: “E’ il popolo stesso che ha bisogno periodicamente di sentirsi raccontare una favoletta per sognare e noi lo accontentiamo”.
Però le elite nulla farebbero se non fossero coadiuvati dai comunicatori. Pensiamo solo a Piero Angela, che mise in onda anni fa sulla RAI ben 9 puntate consecutive di Quark riguardanti il tema delle missioni lunari e planetarie, puntate elaborate su un format acquistato negli USA e trasmesse in prima serata. Solo la tradizione cristiana ci tramanda che la menzogna è, in tutti i casi, figlia del diavolo. Perciò Lei, per molti di noi, non è tanto un eroe, quanto piuttosto quello che un tempo si considerava “uomo dotato del primo requisito della santità”, l’amore per la verità.
Lei ha già selezionato ben 42 domande formidabili, che molti possono capire ed ha evitato ragionamenti più complessi. Ma a volte persino su quelli più semplici la gente risponde: “Mah, io non ci capisco nulla, mentre ci sono fior di fisici e ingegneri che hanno studiato e potrebbero pronunciarsi loro. Perché nessuno di loro dice che si tratta di una bufala?”.
Qui allora proverò ad emularLa su un versante che generalmente non viene percorso dagli alfieri della verità e sul quale invece, nel lontano 1982, l’assistente di Fisica Generale I all’Università portò confidenzialmente me ed altri miei compagni di corso a riflettere poco prima del nostro esame. Ripeto, confidenzialmente, poiché altrimenti avrebbe messo a rischio la sua futura carriera.
Il raggio terrestre è di 6.366 km.
L’orbita massima raggiungibile dallo Space Shuttle è stata dichiarata di 643km, cioè 7.009km dal centro della Terra.
Lassù la forza di gravità è di poco inferiore: è l’82,5%, cioè è calata solo del 17,5%, perché il quadrato del raggio, cioè il denominatore nella formula che la quantifica, è aumentato solo del 21,2%.
Supponiamo ora che la NASA decida che lo Space Shuttle si posizioni su un’orbita dieci volte più ampia, cioè debba raggiungere quota 6.430 km dalla superficie terrestre.
Ecco la forza di gravità, sotto forma di percentuali di quella al decollo (cioè prendendo quella al decollo pari al 100%), che incontrerebbe alle varie quote multiple di 643km, cioè da quota 1 (643 km) fino a quota 10 (6.430 km):
82,5 - 62,2 - 58,9 - 50,7 - 44,1 - 38,8 - 34,3 - 30,6 - 27,4 - 24,8 la cui somma, ricordiamocelo qui sotto, fa 461,3%.
Il lavoro da compiere (energia necessaria) per arrivare sulla prima orbita (quota 643km) è dato dalla forza di gravità per lo spostamento da compiere in senso opposto alla forza. Poniamo qui, per semplicità, di prenderli entrambi, forza di gravità al decollo e quota 643 km, come unità di misura, cioè 1x1=1. Quindi definiamo “unità di energia” quella che serve allo Space Shuttle per raggiungere quota 643 km. In altre parole il lavoro che compiva lo Space Shuttle con un pieno carico di combustibile viene preso pari a 1.
Dunque il lavoro che lo Space Shuttle dovrebbe compiere per arrivare dieci volte più lontano, a 6.430km dalla superficie, sarebbe 4,613 volte superiore a quello che di fatto lo Space Shuttle poteva compiere con il pieno di combustibile. Con un integrale potevamo calcolarlo meglio, ma il risultato sarebbe stato di poco inferiore.
Le missioni Apollo, con il razzo vettore multistadio Saturn V, dovevano chiaramente sfondare quel limite di 6.430 km e raggiungere l’orbita lunare sita mediamente a 378.034 km dalla superficie terrestre (384.400-6.366), cioè addirittura 59 volte più lontano del decuplo dell’orbita massima dello Space Shuttle, vale a dire 590 volte 643km.
Ci basti verificare se erano in grado almeno di sfondare il limite del decuplo.
Le misure dichiarate per lo Space Shuttle furono:
- massa di idrogeno (Serbatoio Esterno) a pieno carico 106 t, avente 15.052.000 MJ (megajoule) di energia spendibile;
- massa di alluminio (combustibile ossidabile) (2 Boosters) a pieno carico 160 t, avente 4.960.000 MJ di energia spendibile;
- massa di polibutadiene-acrilonitrile (combustibile ossidabile) (2 Boosters) a pieno carico 120 t, avente 4.800.000 MJ di energia spendibile;
- totale energia spendibile per la messa in orbita del carico 24.812.000 MJ;
- massa complessiva al decollo 2.030 t;
- totale energia spendibile per tonnellata al decollo 12.223 MJ;
- velocità del Veicolo Orbitale raggiunta al distacco dal Serbatoio Esterno 7,800 km/s;
- massa a pieno carico della navicella del personale (Veicolo Orbitale) 109 t;
- massa a vuoto del Veicolo Orbitale 69 t;
- massa di metilidrazina (combustibile ossidabile) sul Veicolo orbitale 6 t.
Le misure dichiarate per l’Apollo furono:
- massa di idrogeno (Stadi II e III) a pieno carico 87 t, avente 12.354.000 MJ di energia spendibile;
- massa di kerosene RP-1 (Stadio I) a pieno carico 624 t, avente 27.754.650 MJ di energia spendibile;
- totale energia spendibile per la messa in orbita del carico 40.108.650 MJ;
- massa complessiva al decollo 2.970 t;
- totale energia spendibile per tonnellata al decollo 13.505 MJ;
- velocità del Modulo di Comando e Servizio al distacco dal Terzo Stadio 7,793 km/s;
- massa a pieno carico della navicella del personale (Modulo di Comando e Servizio) 30 t;
- massa a vuoto del Modulo di Comando e Servizio 12 t;
- massa di metilidrazina (combustibile ossidabile) sul Modulo di Comando e Servizio 7 t.
Innanzitutto occorre osservare che per entrambi i veicoli si è considerato il combustibile ossidabile della navicella del personale (ivi stivato per manovrarla una volta distaccata dal vettore), come facente parte del carico da mettere in orbita e quindi, sebbene insignificante, è stato qui escluso dal calcolo dell’energia spendibile al decollo per la messa in orbita. Dalle rispettive 6 e 7 t di metilidrazina si possono ricavare 198.000 e 231.000 MJ. Dato che le velocità di rientro delle navicelle sono di poco inferiori a quelle del loro rilascio in orbita da parte dei razzi vettori, l’energia cinetica da perdere per poter rientrare a Terra è di 2.099.000 MJ per il vuoto del Veicolo Orbitale (Space Shuttle), e di 361.000 MJ per il vuoto del Modulo di Comando e Servizio (Apollo).
Dunque il Veicolo Orbitale dello Space Shuttle non poteva perdere velocità solo bruciando metilidrazina e contro-espellendo combusto dai motori, ma si doveva affidare quasi interamente all’attrito dell’aria (con piastrelle di ceramica speciale), mentre il Modulo di Comando e Servizio dell’Apollo ce la poteva quasi fare contro-espellendo combusto di metilidrazina e infatti il suo scudo di atterraggio era di materiale fondibile a perdere, perché l’attrito da sopportare era relativamente poco.
Da quanto sopra si evince però un primo dato importante. Il Modulo di Comando e Servizio dell’Apollo aveva già in partenza una scorta massima di combustibile appena sufficiente alla manovra di rientro in atmosfera e non aveva pertanto il combustibile necessario a distaccarsi dal campo gravitazionale della Luna.
Veniamo ora all’elemento di prova più lampante, cioè che il gruppo formato dal Modulo di Comando e Servizio unito al LEM non poteva neanche raggiungere un’orbita terrestre 10 volte più lontana di quella dello Space Shuttle, per poi continuare verso la Luna.
Infatti dal confronto delle rispettive quantità di energia spendibile per tonnellata al decollo si ricava che il Saturn V con i suoi tre stadi non riusciva a raggiungere quell’orbita, ma poteva giusto attestarsi su un’orbita pressoché uguale a quella del suo successore, lo Space Shuttle. La quasi identica velocità di distacco delle navicelle dai rispettivi vettori conferma ulteriormente questa tesi.
In realtà è da quella medesima quota che il Modulo di Comando e Servizio di Apollo 11 iniziava il collocamento del modulo “LEM”, che altro non era che il primo satellite (o mini stazione orbitale di prova), posizionato in orbita bassa terrestre direttamente da una navicella con personale a bordo, il vero successo per cui a Cape Canaveral esultarono la sera del 20.7.1969.
E’ infatti molto importante notare che la serie Apollo segue la serie Gemini, nella quale si erano testate per la prima volta le due operazioni di rendezvous (avvicinamento) e di aggancio, da parte di una navicella con personale a bordo, ad un satellite già precedentemente messo in orbita, allo scopo di correggerne l’orbita o ripararlo. Con Apollo si testò l’operazione di collocamento in orbita di un satellite avvalendosi di un unico lancio, supportato da tre anziché due stadi propulsori, poiché la navicella con personale a bordo veniva per la prima volta montata sullo stesso razzo vettore insieme al satellite e dunque la loro massa complessiva da mettere in orbita era alquanto superiore.
Con lo Shuttle, l’evoluzione di Apollo e di Gemini, si poté effettuare finalmente le operazioni di correzione, riparazione, posa di satelliti, posa di telescopi ed altre attrezzature, forniture per la Stazione Spaziale Internazionale, posa di lanciatori di satelliti, nonché fare esperimenti di laboratorio a bordo, recuperando l’intera navicella e per giunta impiegando una relativamente infima quantità di combustibile (a vantaggio del carico utile), per farla rientrare, avvalendosi principalmente della forza frenante di attrito delle speciali mattonelle in ceramica.
Nelle accademie queste cose sono risapute, sebbene taciute, perché si rischia il posto, sebbene non sia in gioco la salute delle persone e quindi nessuna multinazionale rischierà mai una condanna a risarcire le centinaia di milioni di telespettatori che scambiarono una sceneggiata per una cronaca. Ora, se le bufale spaziali sono sopravvissute 50 anni, quale accademia, occidentale e non, può dirsi autorevole?
Inoltre per analogia dovremmo pensare che, a maggior ragione su quesiti di importanza vitale (energia nucleare, vaccini, OGM, diserbanti, pesticidi, ecc.) che sono stati posti già alla delibazione accademica, proprio per sgombrare il campo da preoccupazioni riguardanti la salute, si debba credere che in quelle sedi pressioni esterne ancora più forti portino ad anteporre il posto e la carriera alla verità.
Gli accademici che mentono sapendo di mentire su questi temi dovrebbero prima o poi (anche con gli eredi) pagare. Non si può mantenere un ordinamento giuridico che permetta loro di farla così franca. Il tribunale che condannasse l'accademico bugiardo farebbe almeno da contraltare al tribunale che condanna la multinazionale al risarcimento e qualcosa di vero comincerebbe ad emergere.
Cordiali Saluti.
Accedi al sito per partecipare alle discussioni.
Sarebbe in grado di spiegarmi a cosa le serve sommare delle percentuali?
Ecco la forza di gravità, sotto forma di percentuali di quella al decollo (cioè prendendo quella al decollo pari al 100%), che incontrerebbe alle varie quote multiple di 643km, cioè da quota 1 (643 km) fino a quota 10 (6.430 km):
82,5 - 62,2 - 58,9 - 50,7 - 44,1 - 38,8 - 34,3 - 30,6 - 27,4 - 24,8 la cui somma, ricordiamocelo qui sotto, fa 461,3%.
P.S. La prego di non rispondere e evitare di prendere per il naso le persone. Non sono un dottore in fisica ma la fisica di base come questa la comprendo pure io.
Accedi al sito per partecipare alle discussioni.
Il primo problema fondamentale di questo scritto e' ragionare sulla la quantità di energia necessaria in relazione alla distanza dalla terra e a quanta gravità vi e' presente a quella distanza.
La cosa avrebbe senso se stessimo parlando di un ascensore. Che va esclusivamente su e giu'.
Ne' lo Space Shuttle, ne' le missini apollo andavano SU e Giu, qui stiamo parlando di meccaniche orbitali, sottolineo ORBITALI, ovvero:
- Tutti i corpi sono in caduta libera
- Il fatto di non cadere addosso alla terra (o alla luna) dipende da una sola cosa, la velocità laterale ( o orizzontale).
- Si va nello spazio andando veloci, non andando SU
In altre parole: se se in caduta libera e vai abbastanza veloce ORIZZONTALMENTE manchi la terra e sei in orbita, se vai troppo lento "atterri", se vai troppo veloce ti allontani e cerchi di portare la tua orbita ad intersecare quella di un altro corpo (come la luna) e farti catturare.
L'unico momento in cui satelliti, shuttle e razzi in generale vanno VERTICALI sono i primi 80 / 100 KM, lo fanno per togliersi il prima possibile dall'attrito dell'atmosfera terrestre, poi iniziano a mettersi orizzontali finche' non raggiungono la velocità orbitale richiesta, che dipende dall'altezza voluta.
Per andare su un orbita più alta si accelera, per scendere si rallenta (l'orbita non rimane circolare ma si ovalizza verso il lato opposto della terra, serve quindi un'altra manovra per circolarizzarla)
E in tutte queste giravolte il veicolo spaziale e' SEMPRE in caduta libera e sotto il pieno effetto gravitazionale, che diminuisce si con il quadrato della distanza, ma che al lato pratico non interessa: e' tutta una questione di velocità (Delta-V) e di massa.
Fatta questa dovuta premessa andiamo al cuore della questione:
L’orbita massima raggiungibile dallo Space Shuttle è stata dichiarata di 643km, cioè 7.009km dal centro della Terra.
Lassù la forza di gravità è di poco inferiore: è l’82,5%, cioè è calata solo del 17,5%, perché il quadrato del raggio, cioè il denominatore nella formula che la quantifica, è aumentato solo del 21,2%.
Supponiamo ora che la NASA decida che lo Space Shuttle si posizioni su un’orbita dieci volte più ampia, cioè debba raggiungere quota 6.430 km dalla superficie terrestre.
Una quota dieci volte piu' lontana al limite e' di 70.000 KM, 10 volte 7009 KM, l'orbita massima dello shuttle (a pieno carico?)
Ecco la forza di gravità, sotto forma di percentuali di quella al decollo (cioè prendendo quella al decollo pari al 100%), che incontrerebbe alle varie quote multiple di 643km, cioè da quota 1 (643 km) fino a quota 10 (6.430 km):
82,5 - 62,2 - 58,9 - 50,7 - 44,1 - 38,8 - 34,3 - 30,6 - 27,4 - 24,8 la cui somma, ricordiamocelo qui sotto, fa 461,3%.
Quindi? come detto i veicoli non vanno su. Vanno veloci. Integra finche vuoi ma non e' corretto.
Il lavoro da compiere (energia necessaria) per arrivare sulla prima orbita (quota 643km) è dato dalla forza di gravità per lo spostamento da compiere in senso opposto alla forza.
Se fosse un ascensore si, invece nel mondo reale il lavoro da compiere per arrivare all'orbita e' dato dalla velocità necessaria per mantenere quell'orbita vincendo la resistenza della massa da accelerare (che man mano scende quindi serve meno energia a parità di aumento di velocità ) e i primi 100km di attrito dell'atmosfera.
Poniamo qui, per semplicità, di prenderli entrambi, forza di gravità al decollo e quota 643 km, come unità di misura, cioè 1x1=1. Quindi definiamo “unità di energia” quella che serve allo Space Shuttle per raggiungere quota 643 km. In altre parole il lavoro che compiva lo Space Shuttle con un pieno carico di combustibile viene preso pari a 1.
OK
Dunque il lavoro che lo Space Shuttle dovrebbe compiere per arrivare dieci volte più lontano, a 6.430km dalla superficie, sarebbe 4,613 volte superiore a quello che di fatto lo Space Shuttle poteva compiere con il pieno di combustibile. Con un integrale potevamo calcolarlo meglio, ma il risultato sarebbe stato di poco inferiore.
Le missioni Apollo, con il razzo vettore multistadio Saturn V, dovevano chiaramente sfondare quel limite di 6.430 km e raggiungere l’orbita lunare sita mediamente a 378.034 km dalla superficie terrestre (384.400-6.366), cioè addirittura 59 volte più lontano del decuplo dell’orbita massima dello Space Shuttle, vale a dire 590 volte 643km.
No, il ragionamento e' sbagliato sotto molti aspetti, ma quello piu' imbarazzante e' che il razzo non si e' messo in un'orbita CIRCOLARE intorno alla terra alla stessa distanza dalla luna (che richiede molta piu' energia), ma in un orbita fortemente ellittica di intercettazione.
Nelle accademie queste cose sono risapute, sebbene taciute, perché si rischia il posto,
Ci credo che si rischia il posto, se bastano poche ore con un videogioco per capire che il ragionamento non torna, figuriamoci una laurea in astrofisica.
Accedi al sito per partecipare alle discussioni.
Lei considera l'energia esclusivamente Potenziale, il che è un errore molto grave in quanto siamo in presenza della sola forza di Gravità, ossia una forza conservativa, quindi vale il "Teorema di conservazione dell'energia meccanica": la somma dell'energia cinetica e dell'energia potenziale di un punto (il SaturnV non è un punto, ma puo' essere assimilato come tale con la massa che gli diamo noi) che si muove sotto l’azione di forze conservative resta costante durante tutto il moto.
Energia Potenziale (che dipende dalla quota)
L = Integrale da a a b F•ds = + U(ra) - U(rb) = - DU
Energia Cinetica (che dipende dalla velocità)
L = ½m v(exp2) finale - ½m v(exp2) iniziale = Tf - Ti
Il razzo inizialmente ha energia potenziale altissima, immagazzinata come energia chimica del combustibile ed energia cinetica zero. Alla fine dell'ACCELERAZIONE necessaria al razzo per raggiungere LA VELOCITA' DI FUGA (11,2 km/s) avrà energia potenziale molto bassa ed energia cinetica molto alta. Una volta raggiunta la velocità di fuga (it.wikipedia.org/wiki/Velocit%C3%A0_di_fuga) possiamo andare dove le pare senza addurre ulteriore spinta, anche su Marte. Ma finchè sono in presenza di forze conservative l'energia sarà sempre la stessa che avevo quando sono partito.
Mi aspetto che il resto del ragionamento postati da lei sia errato in più punti, come ad esempio sommare le percentuali. Perché?
Questo ragionamento la conduce ad affermare che portare un razzo in quota a 6430 km è energeticamente più dispendioso di 4613 volte rispetto all'energia necessaria che portarlo a 643 km: questa è una BOIATA PAZZESCA perché, come le ho detto prima, siamo in presenza di una forza conservativa (GRAVITA') e il Lavoro speso è proporzionale unicamente alla quota. Quindi se per semplicità di conti facciamo lo sforzo immaginifico di considerare la gravità a 6430km UGUALE alla gravità a 643 km di quota, l'energia spesa sarebbe superiore di 10 volte, non di 4613. Viaggiando verso lo spazio aperto tale lavoro è addirittura inferiore, perché come dice giustamente lei la gravità terrestre si riduce, ma di quanto meno lascio che sia lei a farsi i conti.
Il resto dei dati circa i pesi e i poteri calorifici dei combustibili non mi metto neanche a verificarli perché ad occhio siamo lontani da un ragionamento prettamente scientifico, forse ha frainteso un pelino quell'assistente di fisica. Sono sicuro però che se si rifacesse bene i conti con i nuovi dati che le ho fornito scoprirebbe che alla fine l'uomo, nonostante la sua scarsa evoluzione, sia effettivamente in grado di mandare pezzi di latta nello spazio da quasi 60 anni… uomini non lo so, ma pezzi di latta di sicuro..
Saluti
Accedi al sito per partecipare alle discussioni.
Costoro potevano effettivamente rilevare una mia taciuta congettura, che non riguardava, né la forma dell’orbita (ellittica o circolare), né la velocità di fuga che attiene pur sempre ad un’orbita ellittica, come quella delle comete ricorrenti.
Nella mia dissertazione iniziale l’assunto che il lavoro compiuto dallo Space Shuttle per raggiungere quota 643 km dalla superficie terrestre fosse 1x1, cioè forza di gravità presa come unitaria moltiplicato la distanza presa come unitaria, poteva obbiettare che nella realtà la forza di gravità agente sul veicolo diminuisce via via che le masse del combustibile e dell’ossidante fuoriescono combinate dai motori, fino ad esaurirsi una volta raggiunta tale quota. Dunque qualcuno poteva obbiettare che l’energia necessaria allo Space Shuttle per raggiungere quota 643 km è inferiore a quella da me ipotizzata.
Tuttavia il mio ragionamento non cambia, perché io ho assunto come unitaria proprio questa energia a prescindere da come si è arrivati a calcolarla. E ho concluso che per raggiungere quota 6.430 km occorreva 4,613 volte quella energia (non ho scritto 4.613 volte, siamo in Italia e vale la virgola prima dei decimali).
Cioè ho ipotizzato che da quota 643 km a quota 6.430 km lo Space Shuttle proseguisse con i serbatoi scarichi ed un angelo gli fornisse, istante dopo istante, il combustibile e l’ossidante necessari a proseguire il viaggio.
Se volessimo fare a meno dell’angelo, cioè se volessimo realizzare concretamente l’operazione di messa in orbita a 6.430 km dovremmo caricare serbatoi aggiuntivi prima del decollo, ma a quel punto dovremmo ricalcolare l’energia necessaria a raggiungere quota 643 km e ci accorgeremmo che è aumentata proporzionalmente all’aumento del carico, poiché uno dei suoi due fattori, la forza di gravità, è aumentata proporzionalmente all’aumento del carico. Dunque lo Space Shuttle per raggiungere quota 6.430 km senza l’angelo erogatore consumerebbe una quantità di energia molto superiore a 4,613 volte quella impiegata per raggiungere quota 643 km.
Ciò vale di pari passo anche per l’energia impiegata per tonnellata al decollo, che è la grandezza su cui abbiamo focalizzato l’attenzione per fare un confronto con l’Apollo.
Quindi dopo questa precisazione la mia tesi risulta rafforzata.
Accedi al sito per partecipare alle discussioni.
Mi pare di ricordare che aerei e razzi funzionino con una variabile chiamata "spinta", le dice nulla?
prendendo la variabile "x" come energia necessaria a compiere il Lavoro di portare il razzo a una quota, cos'è che non le torna di quell'energia? Sta immagazzinata nel combustibile e viene trasformata in Spinta che dà Velocità al vettore.
Se io riempio un treno merci di combustibile per razzi avrei l'energia per andare su Giove, ma difficilmente ci arriverei, dico bene?
La spinta generata da uno shuttle in decollo (SRB + Vettore + ET), a memoria, mi pare fosse sui 30 milioni di Newton.
Quella del Saturn V era molto di più: circa 34.000 kN al primo stadio, circa 4000kN al secondo e circa 1000 kN al terzo.
Per generare quella spinta non si puo' dare fuoco al combustibile tutto in una volta, ci sono altre variabili, come la forma degli ugelli dei razzi. Ridurla a un semplice bilanciamento di energia è riduttivo quanto affermare che siccome l'energia immagazzinata dentro una Ferrari e una Panda sia la stessa (40 litri di benzina), allora raggiungeranno lo stesso traguardo: Manco per il cazzo! La panda farà 700/800 km, la Ferrari forse 150/200. Eppure hanno la stessa energia!
Conta la Spinta per raggiungere la Velocità di fuga e andare nello spazio
Dove sta la spinta nel suo ragionamento?
Se per lei Velocità e Spinta non contano nulla le consiglio un paio di testi e la discussione finisce qui.
Facciamo così, se vuole una risposta da parte mia le chiederei la gentilezza di eliminare tutte le parole dal suo post e di spiegarsi usando solo formule intervallate da parole tipo "dato che", "siccome", "allora", "dunque".. e volendo al massimo un paio di righe di considerazioni.
io ragiono meglio così (ed evitiamo fraintendimenti e supercazzole che fan perdere tempo)
Saluti
Accedi al sito per partecipare alle discussioni.
- CharlieMike
-

- Offline
- Platinum Member
-

Registered
- Messaggi: 2950
- Ringraziamenti ricevuti 435
OTMO62 ha scritto: (non ho scritto 4.613 volte, siamo in Italia e vale la virgola prima dei decimali).
Se vuoi evitare fraintendimenti non mettere il punto di separazione delle migliaia, ma solo la virgola decimale.
Fine OT
Accedi al sito per partecipare alle discussioni.
Questa è evidentemente una sciocchezza, dato che la velocità di fuga è per definizione la velocità necessaria per imprimere ad un oggetto una traiettoria parabolica che si allontana indefinitamente dal corpo celeste considerato, nel nostro caso la Terra. E' noto che la velocità di fuga è √2 volte la velocità orbitale a "quota zero", ne segue (passando all'energia cinetica del corpo) che l'energia necessaria ad allontanare indefinitamente un oggetto è il doppio di quella che occorre per immetterlo in un'orbita bassa. Trascurando l'esistenza dell'atmosfera, ma ci arrivo tra un attimo.MO62 ha scritto: Chiedo cortesemente ai partecipanti di non eludere la questione.
Costoro potevano effettivamente rilevare una mia taciuta congettura, che non riguardava, né la forma dell’orbita (ellittica o circolare), né la velocità di fuga che attiene pur sempre ad un’orbita ellittica, come quella delle comete ricorrenti.
Basterebbe questo per chiudere la questione, ma nel ragionamento iniziale ci sono anche due grossi errori di fondo. Il primo, già segnalato da altri, è che si considera solo l'energia potenziale gravitazionale, cioè in pratica non stiamo parlando di razzi ma di un ipotetico ascensore che porta alla quota "h" una certa massa, mentre un satellite per restare stabilmente in orbita ha bisogno di essere alla quota h con una certa velocità v, dipendente da h. Il secondo errore è invece per l'appunto trascurare quel dettaglio che è l'atmosfera terrestre, quando invece è risaputo che la maggior parte dell'energia necessaria a mandare in orbita qualcosa è proprio spesa per lasciare l'atmosfera alla corretta velocità.
Comunque, prendendo come quota di riferimento 643 km sopra la superficie, e considerando solo l'energia potenziale gravitazionale, ossia nel caso dell'ascensore "spaziale", la quantità di energia spesa per portare 1 kg a tale quota è 5.73 MJ. Se i numeri riportati nel primo post di @MO62 sono corretti (non ho nessuna intenzione di verificare), abbiamo per lo Space Shuttle 24 812 000 MJ di energia totale disponibile al decollo, a fronte dei "soli" 5.73*109 000 = 624 000 MJ necessari per dislocare alla quota di 643 km le 109 tonnellate della navetta a pieno carico. Dovrebbe essere evidente che questo modo di ragionare non porta da nessuna parte, infatti: che fine hanno fatto quei 24 milioni e rotti di MJ in eccesso stipati nei serbatoi? Sono andati tutti per accelerare le 2000 tonnellate di massa al momento del lancio (le quali via via che il combustibile bruciava e i razzi si sganciavano diminuivano) alla corretta velocità orbitale. Ma a questo punto, cioè con 109 tonnellate di Shuttle in orbita a 643 km di quota, "basterebbe" fornirgli ulteriori 3 000 000 MJ (pari alla sua energia cinetica) per accelerarlo fino alla velocità di fuga e spedirlo ovunque nel sistema solare.
Aggiungo una precisazione: anche io penso che con ogni probabilità il razzo Saturn non avesse la potenza necessaria per portare in orbita lunare la nave Apollo, nè che poi questa avesse sufficiente carburante per rientrare sulla terra, ma l'argomentazione esposta sopra non dimostra proprio niente di tutto ciò. Io mi baso su un confronto con le missioni lunari sovietiche, che - dopo molti fallimenti - riuscirono ad eseguire la manovra con sonde automatiche dal peso risibile che rispedirono sulla terra una manciata di grammi di campioni. Anche senza considerare la presenza di astronauti delle missioni Apollo, con tutte le complicazioni e implicazioni del caso, già solo in termini di masse da gestire siamo su ordini di grandezza completamente differenti, e siccome prima e dopo di allora la scienza astronautica sovietica è sempre stata al passo se non avanti rispetto a quella americana, sorgono molti dubbi sulle reali capacità del vettore della NASA.
FranZη
Accedi al sito per partecipare alle discussioni.
- DanieleSpace
-

- Offline
- Senior Member
-

Registered
- Una volta ero certo. Ora sono pieno di dubbi
- Messaggi: 379
- Ringraziamenti ricevuti 65
Io non sono in grado di argomentare ulteriormente, ci avevo provato in un altro post, chiamato "Chi ha il razzo piccolo" , dove volevo verificare se il LEM avesse carburante sufficiente per decollare, orbitare e rientrare verso Terra. Discussione poi arenatasi per mancanza di informazioni e di tempo da parte mia.
Mi sorge però una domanda. Visto che esistono diversi simulatori di meccanica orbitale e di razzi spaziali, sapreste dire se esiste una simulazione (magari su youtube) il più completa possibile che mostri l'applicazione di quanto affermato nelle missioni Apollo ? Cioè, oggi dovrebbe essere relativamente semplice inserire tutti i dati nel simulatore e verificare se il tutto è fattibile con le misure, il peso e i tempi delle missioni Apollo. Esiste qualcosa del genere ? Qualcuno ci è andato anche solo vicino ?
Una teoria del complotto è ridicola solo quando sono ridicoli i suoi moventi.
Accedi al sito per partecipare alle discussioni.
consiglio di provare Kerbal Space Program, un gioco davvero divertente che simula con precisione pesi, potenze e masse....di Kerbin, un ipotetico pianetino. Non ci sono simulatori spaziali realistici a poco prezzo...
Pero' puoi moddare KSP all'infinito per renderlo il piu' realistico possibile, ma secondo me e' divertente giocare gia cosi', ti forza a ragionare su massa e carburante e costruire il tuo razzo su misura per la missione
forum.kerbalspaceprogram.com/index.php?/...l-v1250-08-jan-2019/
Accedi al sito per partecipare alle discussioni.
- kamiokande
-

- Offline
- Premium Member
-

Registered
- Messaggi: 488
- Ringraziamenti ricevuti 158
history.nasa.gov/SP-4029/Apollo_11h_Transearth_Phase.htm
è di 3279ft/s ovvero circa 1000m/s. Considerando che la manovra alla Hohmann è quella che richiede meno consumo di carburante e che le missioni Apollo non hanno usato manovre alla Hohmann, direi che il valore riportato è decisamente consistente (mi stupirei del contrario). Ora con i dati del motore del CSM, l'AJ10-137, che troviamo su wikipedia
en.wikipedia.org/wiki/AJ10
Usando l'equazione di Tsiolkovsky si può calcolare la massa di combustibile bruciata per ottenere il DV riportato (1000m/s), che è di circa 7900kg. Considerando che la quantità di combustibile imbarcata è circa il doppio di quella consumata nella manovra di ritorno, e che per l'andata la totalità dell'impulso per arrivare sulla Luna è stato dato dallo stadio S-IVB del Saturn V, direi che la cosa è, dal punto di vista dei numeri, fattibile.
"La stampa è morta" (Egon Spengler - Ghostbuster)
Accedi al sito per partecipare alle discussioni.
- kamiokande
-

- Offline
- Premium Member
-

Registered
- Messaggi: 488
- Ringraziamenti ricevuti 158
"La stampa è morta" (Egon Spengler - Ghostbuster)
Accedi al sito per partecipare alle discussioni.
Affinché l'insieme del Modulo di Comando e Servizio (30 t) più LEM (15 t), una volta acquisita l'orbita bassa terrestre, raggiungesse la velocità di fuga occorreva che un angelo erogatore gli fornisse propellente durante l'ulteriore accelerazione, per raddoppiare la sua energia cinetica.
L'energia cinetica in bassa orbita terrestre era 0,5*45.114*7.793*7.793/1.000.000 = 1.369.906 MJ
Per fornire altrettanta energia l'angelo erogatore avrebbe dovuto rifornire in corsa, lungo la famosa "Trans Lunar Injection", la bellezza di 9,6472 t di idrogeno e 77,1776 t di ossigeno, cioè circa 87 t di propellenti, tirandosi dietro con la forza delle sue ali il serbatoio (pesante almeno altre 10 t), per un totale di 97 t.
Vogliamo ancora discutere?
Accedi al sito per partecipare alle discussioni.
- kamiokande
-

- Offline
- Premium Member
-

Registered
- Messaggi: 488
- Ringraziamenti ricevuti 158
Non sai di che cosa parli. Quando si parla di cambiamenti orbitali si parla di DeltaV e di Impulsi specifici. I DeltaV necessari per l'andata sono di circa 3000m/s, e per il ritorno sono di circa 1000m/s . Alla fine parliamo di qualche migliaia di kg di propellente, se a te la cosa pare impossibile non so cosa dirti.
"La stampa è morta" (Egon Spengler - Ghostbuster)
Accedi al sito per partecipare alle discussioni.
In breve: un certo buon senso "istintivo" mi induce a ritenere che l'atterraggio di un razzo "sulla coda" - à-la SpaceX - sia, se non impossibile, per lo meno irragionevole tenendo conto dei carichi aggiuntivi per il carburante e per i molteplici motori direzionali, dell'incremento esponenziale della difficoltà di controllo missione e del "mirabolante" testa-coda da effettuare dopo il rientro in atmosfera.
Al mio scetticismo su tutto il fenomeno Elon Musk aggiungo l'evidente manipolazione CGI dei video delle missioni SpaceX.
Secondo voi è verosimile l'affaire SpaceX o siete del mio stesso parere?
Grazie in anticipo a chi vorrà rispondermi.
Accedi al sito per partecipare alle discussioni.
- kamiokande
-

- Offline
- Premium Member
-

Registered
- Messaggi: 488
- Ringraziamenti ricevuti 158
Benché la cosa sia decisamente complessa non è affatto impossibile. Ti ricordo il DC-X della McDonnel-Douglas di metà anni novanta e che doveva sostituire lo shuttle
Oppure il New Shepard di Blue Origin
"La stampa è morta" (Egon Spengler - Ghostbuster)
Accedi al sito per partecipare alle discussioni.
Anche qui si parla tanto di pesi, traiettorie ecc..
È più sensato o anche queste asserzioni sono incorrette ?
Accedi al sito per partecipare alle discussioni.
Il che significa anche che, se soltanto l'avessero voluto, gli americani avrebbero potuto tranquillamente organizzare un'ulteriore spedizione di "ricognizione" intorno alla Luna con una delle tante missioni dello Shuttle, utilizzandolo come "intermediario", ovvero per portare in orbita terrestre una piccola navicella, alla quale sarebbe stato aggiunto un razzo (fatto arrivare in orbita con un differente vettore) per il tragitto di andata e ritorno dalla Luna (ed è strano che in oltre vent'anni di Shuttle la cosa non sia stata fatta)...
Accedi al sito per partecipare alle discussioni.
- Cum grano salis
-

- Offline
- Senior Member
-

Registered
- Se l'avrei saputo, mo' te l'imparavo ;-)
ho riletto più volte i suoi post per essere abbastanza sicuro di aver capito bene cosa intendesse dire. Spero di aver trovato il bandolo della matassa ed ora le dico la mia, non prima di alcune doverose premesse che ritengo assolutamente necessarie in virtù di altre spiacevoli vicende in cui sono incorso in passato :
1. userò il "tu" per maggiore immediatezza di scrittura, ed anche perché le parlerò come fossimo in amicizia davanti ad una birra fra amici e non ad un simposio formale : siamo pur sempre in un forum e non in cattedra, e qui si usa così :-)
2. dovrò per forza di cose introdurre concetti banali di fisica che già conosce bene, ma non so se ha mai affrontato anche questioni ingegneristiche sull'argomento : ciò mi è inevitabile se voglio argomentare un minimo, inoltre la lettura potrà essere più agevole anche per chi non dovesse avere che delle reminiscenze scolastiche.
Non intendo quindi in nessun modo sembrare o anche solo apparire vagamente un qualcuno che ha la presunzione di insegnarle niente di niente, ma solo cercare di inquadrare il discorso affinché lei possa successivamente proseguire in autonomia nei ragionamenti ed eventualmente nei calcoli (motivo per cui non ne farò neanche uno di quelli che contano veramente per i suoi scopi di verifica). Il "secondo me" deve essere inteso e sottointeso ovunque, benché non lo dirò mai per semplicità, tranne la prima volta.
Questo punto numero 2 è un assioma indiscutibile ed indimostrabile, deve essere un paletto concettuale fisso ed inamovibile per tutti, altrimenti è inutile proseguire (oltre ad essere estremamente dannoso il volerlo ignorare consapevolmente e di proposito).
3. sto scrivendo di getto per motivi di tempo, e mentre leggo di nuovo i suoi post (quindi potrei non seguire un filo logico), e parlerò di argomenti che risalgono a studi di ben più di due decenni fa, e che nel frattempo colgo l'occasione per ripassare. Se scrivo castronerie, cosa possibilissima, gradirei poi non essere messo in croce e rubare così la scena a qualcun altro alla messa di domani (sto scherzando :-) , ma fino ad un certo punto). Se qualcosa non va, ne riparliamo con calma.
4. quello che andrò a scrivere non vuole essere una presa di posizione, neanche velata, sulla realtà o meno di una o più missioni Apollo. Ci sono già discussioni e thread a non finire sull'argomento, qui ed in rete, che discutono un'infinità di altre questioni molto più interessanti. [Per inciso, e tra parentesi quadre ad evidenziarne ulteriormente la dicotomia, io sono convinto che l'uomo sia già in grado da molto tempo di muoversi agilmente nello spazio-tempo, attraverso l'uso di conoscenze e tecnologie che non si trovano nei libri di testo ufficiali o che hanno consensus scientifico, ma siccome non ne ho le prove 'provate', le parlerò attraverso testi e riferimenti alla conoscenza a noi tutti familiare, che è poi quella con cui abbiamo a che fare tutti i giorni, e che funziona bene direi nella nostra realtà quotidiana, a prescindere dall'altra molto più avanzata e diversa, sia concettualmente che tecnologicamente. Tengo ben separati i due aspetti della cosa, in attesa di un futuro che eventualmente li unifichi, se mai ci sarà]
Innanzitutto, ad occhio, visto che forse non se n'è accorto nessuno, ci dovrebbe essere un errore di battitura nella serie relativa alle percentuali che hai postato, non mi torna la dinamica della progressione numerica nel secondo valore, che penso si avvicini più al 70% che al 60%. Non è che abbia importanza, ma nel caso tu dovessi ripostare la discussione altrove ti consiglierei di controllare prima. Ho capito il senso dell'uso della sommatoria delle percentuali, benché normalmente sia un'operazione rischiosa come ricordava FranZeta altrove luogocomune.net/LC/forum/cose-frivole/31...acca2o?start=0#10046 , quindi parto da lì.
Mi limito ai primi due valori, tanto per i successivi il discorso sarebbe il medesimo, ma l'inghippo si trova nei primi due, secondo me (vedi punto 2). La quantità di energia necessaria a sollevare un oggetto fermo dalla superficie terrestre da un punto A ad un punto B, in questo caso non può essere considerata uguale a quella successiva da B a C del tuo esempio. Come è già stato detto da altri, stai ragionando in termini di campo conservativo puro, considerando gli stati iniziali e finali dell'energia, però non stai mettendo in mezzo anche le altre energie e le altre forze coinvolte nella modellizzazione del problema. Quando il razzo è fermo a terra, per farlo sollevare, prima ancora che accelerarlo, bisogna vincere la forza peso e l'inerzia della sua massa. Fatto questo prima, e proseguendo poi, una volta giunto alla quota della sua prima orbita, siamo in una diversa condizione di equilibrio : se guardiamo da "dentro" il razzo, la forza peso della struttura e di quello che c'è dentro è adesso bilanciata dalla forza centrifuga, cosa che prima non avveniva, ed ora abbiamo a che fare solo con l'inerzia della massa. O meglio, le manovre di trasferimento orbitale successive avvengono in genere in direzione tangente alla traiettoria orbitale, in modo da annullare (o minimizzare) le perdite gravitazionali, in quanto la spinta è sempre (o quasi) perpendicolare alla forza di gravità. Un po' come gli astronauti sulla ISS che non fanno di certo lo stesso sforzo ad alzarsi in piedi che fanno sulla Terra (lo so che lo sai bene, lo dico per chi dovesse leggere e magari sia convinto erroneamente dal modo di dire che "nello spazio", inteso come in orbita intorno alla Terra, non ci sia, tout court, la gravità come forza esistente).
Capisci bene che quindi, una volta giunti in orbita, è tutto un altro discorso avere a che fare 'solo' con l'inerzia, enormemente diminuita poi rispetto alla partenza, visto il grande consumo di 'combustibile' (in senso lato) che man mano non c'è più, e lo sgancio degli stadi del razzo necessari al raggiungimento della quota prevista. Le condizioni di partenza da Terra (A) e quelle di ri-partenza dall'orbita (B) verso un'altra orbita (C), sono completamente differenti oltre alla diversa gravità e non paragonabili fra loro a meri fini energetici in maniera così semplificata.
Quota prevista, dicevo, a cui corrisponde una ben nota velocità orbitale. Questa velocità, però, è calcolata rispetto al centro di riferimento inerziale in cui si considera la Terra fissa. Ma sappiamo bene noi non terrapiattisti :-) che la Terra, pur considerata fissa, sta ruotando su se stessa, quindi al momento della partenza il razzo ha una sua velocità tangenziale che è funzione della latitudine del punto di lancio, motivo per cui si cerca di massimizzare questa velocità cercando di partire da luoghi quanto più vicini all'equatore, puntando poi la traiettoria di volo verso Est, quindi in verso positivo alla rotazione (salvo i casi particolari di satelliti con orbite retrograde). La latitudine scelta, di contro, però poi incide sull'inclinazione massima dell'orbita, ma avrai modo di approfondire facilmente dopo con le dispense. Quindi, sfuttando quanto più possibile la velocità tangenziale di partenza (che all'equatore è di circa 465m/s), alla velocità orbitale di riferimento che dobbiamo ottenere spendendo energia possiamo e dobbiamo togliere la velocità di partenza che già abbiamo in partenza per il solo fatto di ruotare insieme alla Terra.
Inoltre è sempre bene distinguere nei ragionamenti tra energia potenziale gravitazionale ed energia potenziale chimica. I termini di energia potenziale ed energia chimica sono più facilmente identificabili ed aiutano a non commettere errori concettuali o fraintendimenti logici. Inoltre la quantità di energia (chimica) per tonnellata al decollo, già solo cambiando un singolo motore prima ancora che numero di stadi e/o loro uso fra due lanciatori diversi, porta a conclusioni totalmente fuori strada. La dinamica è molto più complessa di un semplice rapporto di energia/peso di partenza (ad es. ugello sovra o sotto espanso, se non adattato, per quote diverse, per dirne una sola fra mille), ed è fatta di step successivi oltre a variazioni continue di rapporti di forze e masse/pesi in gioco. Si può fare forse un discorso finale riassuntivo di quanti kg di propellente siano necessari per mandare 1kg 'verso' la Luna (non 'sulla' Luna, e sono circa 50kg mi sembra).
Le tonnellate di propellente che ti mancano nel raddoppio di energia cinetica tra orbita di parcheggio e Trans lunar injection sono ovviamente all'interno dell'S-IVB. Da en.wikipedia.org/wiki/S-IVB abbiamo un peso lordo di 115 ton., di cui 105 ton. di propellente totale (da cui quindi circa 10 ton. di struttura), di cui la parte residua post immissione in orbita bassa è stato consumato riaccendendo il motore per 346 sec. a fronte di un massimo tempo totale utilizzabile di circa 500 sec. del motore J-2 en.wikipedia.org/wiki/Rocketdyne_J-2 Da history.nasa.gov/SP-4029/Apollo_11d_Ascent_Phase.htm vediamo che per l'immissione in orbita bassa è rimasto acceso la prima volta per 147 sec. In totale, quindi, 493 sec.
E' possibile però dare un'occhiata a dati più precisi nel report di valutazione post volo dell'Apollo 11 :
www.ibiblio.org/apollo/Documents/lvfea-AS506-Apollo11.pdf
(o del volo precedente dell'Apollo 10 per un confronto eventuale
ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19700026422.pdf )
Dal report si ricava da pag.99 del pdf, che il consumo medio nella prima accensione è stato di 214 kg/sec di propellente.
E si ricava da pag.108, che il consumo medio nella seconda accensione è stato di 212 kg/sec.
Tra prima e seconda accensione, in totale, sono stati consumati 214 x 147 + 212 x 346 = 31458+73352 = 104810 kg cioè quasi 105 ton., per cui direi che ci siamo. Ci sono tonnellate da consumare per il prima e ci sono per il dopo, visto che è l'S-IVB a fornire la spinta per il Trans lunar injection. Non vi è un'erogazione aggiuntiva ed ipotetica in corsa, come sostieni, era previsto che si accendesse di nuovo una seconda volta utilizzando il propellente residuo, dimensionato alla bisogna più un certo margine di sicurezza minimo per via del peso aggiuntivo.
Accedi al sito per partecipare alle discussioni.
- Cum grano salis
-

- Offline
- Senior Member
-

Registered
- Se l'avrei saputo, mo' te l'imparavo ;-)
Non si parla solo di spinta, visto che il consumo di combustibile è limitato, e lo si può utilizzare per un certo tempo in totale.
Introduco meglio quest'ultimo concetto un po' ostico dilungandomi molto, perché è fondamentale per capire di cosa si parla quando ce lo troviamo davanti parlando di Δv (più in là, nelle fonti) : (mi risparmio un bel po' di fatica copiando da www.forumastronautico.it/t/differenza-tr...ulso-specifico/16378 )
Qual è la differenza tra spinta e impulso specifico?
R.1 La spinta è ciò che determina la causa del moto; è quindi una forza e - in termini matematici - entra nell’equazione della dinamica (o di Newton, in pratica SPINTA + altre forze = massa * accelerazione) da cui si può ricavare l’accelerazione. In sostanza la forza di espulsione dei gas di un endoreattore, per reazione, ti dà la spinta, nella direzione del moto stesso (in prima approssimazione).
L’impulso specifico è la spinta diviso la portata ponderale in massa del propellente consumato: si misura in secondi per l’infelice definizione di “ponderale” anzichè “massica”. In sostanza è una caratteristica del propulsore: valori molto alti di Isp implicano bassissime portate in massa (motori a ioni ad esempio, dove vengono espulsi pochi ioni per volta), mentre per i propulsori di accesso allo spazio si hanno alte spinte ed alte portate in massa, con il rapporto che arriva a 250 - 350 secondi.
In sostanza quindi, per una determinata manovra serve una certa accelerazione che viene fornita creando una spinta in un tempo voluto, ma per scegliere il propulsore corretto occorre guardare anche il suo impulso specifico: più è alto, e più si passa ai propulsori elettrici e al plasma.
R.2 La spinta in sostanza è la forza vera e propria con cui il propulsore spinge il veicolo, e quindi si misura in Newton.
L’impulso totale è l’integrale della spinta del propulsore nel tempo di funzionamento. Per farla semplice, se la spinta fosse costante durante tutto il tempo in cui il propulsore è acceso, l’impulso totale sarebbe la spinta moltiplicata per il tempo in secondi. Se la spinta non è costante nel tempo invece, il calcolo va appunto fatto con un integrale. La sua unità di misura sono quindi Newton x Secondo.
L’impulso specifico è definito come il rapporto tra l’impulso totale e il peso di propellente consumato. Quindi in termini semplici indica quanto un propulsore consuma per fornire una determinata spinta per un determinato tempo. Più è alto l’impulso specifico e meno il propulsore consuma. L’unità di misura è quindi data da Newton x Secondo / Newton, quindi Secondi.
In realtà, per essere più precisi, l’impulso specifico è il rapporto tra l’impulso totale e il peso che il propellente consumato avrebbe sulla superficie terrestre. Il motivo è che ovviamente non si vuole che le caratteristiche di un propulsore dipendano da dove si prenda la misura (in orbita, su Marte o chissà dove). Per cui la formula per il calcolo sarà Isp = Itot / (m x g0), in cui m è la massa di propellente consumata e g0 è 'l'accelerazione di gravità terrestre standard' [N.d:R. ho corretto io, fra gli apici, la svista].
A questo punto prendiamo l’equazione del razzo: T = mpunto x c (mpunto è massa/tempo, ovvero la portata massica al secondo, e c è la velocità di uscita del propellente). Avremo quindi che l’impulso totale sarà Itot = mpunto x c x tempo (dove t è il tempo di accensione). Chiaramente mpunto x t = m/t x t, e quindi Itot = m x c.
Da qui viene facile che Isp = (m x c) / (m x g0) = c / g0. Ed ecco fatta la magia! L’impulso specifico è pari alla velocità di uscita del propellente dal razzo diviso per la costante gravitazionale terrestre.
Approssimando g0 a circa 10, avrai quindi che l’impulso specifico misurato in secondi è pari a circa 'un decimo' la velocità di uscita del propellente (N.d.R. ho corretto io la svista originale mettendola fra gli apici anche qui). E quindi, rigirando la frittata, a parità di spinta, più velocemente il propellente esce dal razzo e meno saranno i consumi.
Per questo motivo, essendo l’Isp in secondi un pò difficile da visualizzare mentalmente come una grandezza, la costante g0 viene spesso dimenticata, e si tende ad indicare l’impulso specifico semplicemente come una velocità. E per questo motivo frequentemente lo si trova indicato in m/s invece che in secondi.
R.3 L’impulso specifico (o la velocita’ equivalente di efflusso dei combusti che è proporzionale ad esso) è un fattore importantissimo, che compare nell’equazione dei razzi:
it.wikipedia.org/wiki/Equazione_del_razzo_di_Ciolkovskij
Per una manovra orbitale lontano da un forte campo gravitazionale, l’Isp è la cosa più importante. Più è grande e più e basso il rapporto di massa, e quindi il consumo di propellente per ottenere un certo delta V.
E questo è abbastanza noto.
Però spesso si sottovaluta l’importanza del rapporto spinta/peso per manovre all’interno di campi gravitazionali intensi, in primis per un lancio dalla superficie terrestre all’orbita ma non solo.
Basti dire questo: se un razzo ha un T/W inferiore a 1 non si stacca neanche da terra, pur consumando tutto il propellente.
Per T/W bassi, diciamo sotto 1.5, le cosiddette gravity losses sono molto elevate. In termini intuitivi possiamo dire che il veicolo spreca gran parte della sua spinta per librarsi nell’aria più che per accelerare e guadagnare quota.
Perché dico questo? Perché spesso si pensa che un razzo nuclere, avente un Isp molto elevato, potrebbe rendere possibile astronavi in grado di staccarsi da terra e andare in orbita con rapporti di massa molto bassi… come nella fantascienza. Niente di più sbagliato.
Anche lasciando perdere le questioni di costo, sicurezza e inquinamento i motori nucleari ipotizzati fino ad ora sono pesanti, molto pesanti, e hanno un rapporto T/W basso. In pratica questo rende impossibile che volino o, nella migliore delle ipotesi, invalida il vantaggio dell’Isp più elevato.
[...]
Faccio notare che il T/W non è importante solo per la messa in orbita. Esistono molte manovre spaziali che richiedono una spinta relativamente forte in tempi relativamente brevi, che i motori elettrici a ioni non possono dare.
Il caso più eclatante è lo sfruttamentro dell’effetto Oberth :
en.wikipedia.org/wiki/Oberth_effect
Provo a dirlo in modo semplicistico e mi scuso in anticipo per imprecisioni e semplificazioni : se devo accellerare un veicolo spaziale si può dimostrare che se fornisco un certo impulso mentre è vicino ad un corpo molto massivo (tipicamente un pianeta o il sole) dove il potenziale gravitazionale è basso e la velocita’ più alta ottengo una velocita’ finale molto più elevata che se fornisco lo stesso impulso mentre è nello spazio profondo.
Insomma, se devo accelerare una sonda può essere che con un piccolo impulso con motori chimici durante il fly-by di Giove ottengo un risultato migliore che con un impulso più grande con un motore a ioni che avendo una spinta molto bassa non può sfruttare l’effetto Oberth.
Guardate che non è roba da poco. Nell’esempio riportato da Wikipedia, con un impulso di solo 5 km/s durante un fly-by di Giove ottengo una velocita’ finale di oltre 22 km/s… con una moltiplicazione di delta V di 4.6 volte a parita’ di propellente utilizzato.
Lo stesso se devo alzare l’orbita ellittica di un satellite intorno alla Terra. Se spingo solo mentre sono più vicino al perigeo, dove il satellite è basso e veloce, l’effetto finale viene moltiplicato.
L’astrodinamica è molto complessa e molti effetti sono anti-intuitivi… diciamo che anche per una manovra orbitale disporre di un motore che spinge tanto in poco tempo può essere molto utile e dar luogo a traiettorie molto più efficienti.
Accedi al sito per partecipare alle discussioni.
- Cum grano salis
-

- Offline
- Senior Member
-

Registered
- Se l'avrei saputo, mo' te l'imparavo ;-)
Per ovvi motivi di sicurezza, cioè non perdere gli astronauti nello spazio in caso di problemi, non era di certo il caso di 'spararli' alla velocità di fuga propriamente detta. Dai documenti precedenti sappiamo che la quota in orbita bassa è di circa 100 miglia nautiche, cioè 185 km. Partendo da un raggio della Terra di 6371km + 185km = 6556 km, abbiamo una velocità di fuga di 11,027 km/sec. it.wikipedia.org/wiki/Velocit%C3%A0_di_fuga
Sappiamo da history.nasa.gov/SP-4029/Apollo_11f_Translunar_Phase.htm che la velocità finale di uscita dall'orbita di parcheggio verso la Luna è di 35.545,6 ft/sec. e cioè 10,834 km/sec., e la successiva Midcourse correction aggiunge appena 20 ft/sec. e cioè 6 mt/sec. ed è ininfluente per questi fini (20 km/hr in più, per capirci).
Inoltre la traiettoria scelta consente l'eventuale free return en.wikipedia.org/wiki/Free-return_trajectory , almeno fino all'Apollo 14 credo, cioè il ritorno a casa in caso di problemi senza aver bisogno dell'uso dei motori, una volta fatto il giro intorno alla Luna (cosa poi sostanzialmente avvenuta con l'Apollo 13 che ha usato per pochi secondi ed a meno della metà della potenza il motore del LEM, per quel che ricordo).
Attraverso un'approccio che prevede il passaggio "davanti" alla Luna, cioè dal lato che fronteggia il suo incedere nel percorso di rivoluzione intorno alla Terra, sfruttando l'assistenza gravitazionale dell'effetto fly-by, si ottiene un certo rallentamento dell'Apollo senza consumo di propellente (poco peso in meno risparmiato, ma sempre utile in questi casi), finché poi non si frena ulteriormente con il motore per l'ingresso nell'orbita Seleno-centrica history.nasa.gov/SP-4029/Apollo_11g_Lunar_Orbit_Phase.htm
Spero di non aver fatto confusione e scritto fesserie madornali a tarda notte, pur essendo una cosa veloce (che poi non lo è stata affatto alla fine...) e necessariamente breve
Questo Pdf che ho ritrovato nel pc, è di un mio collega dei tempi del Columbus, credo, che aveva fatto un bel riassunto nel trentennale dell'Apollo 11 :
drive.google.com/file/d/1MQdtpSgWFBELNUw047D0gIHAoWk9KXMF/view
qui invece qualche dato complessivo e foto in più
pselab.chem.polimi.it/wp-content/uploads/2014/07/Apollo-11.pdf
Ora invece delle dispense vere e proprie di Propulsione Aerospaziale, molto chiare per quel poco che ho potuto leggere, molto sintetiche come usa ora col nuovo ordinamento, ma che richiamano anche altri concetti che ho dovuto tralasciare per forza di cose e che servono per inquadrare ancora meglio il discorso
dma.ing.uniroma1.it/users/aeroprop_c2/pa04.pdf
Di esercizi ce ne sono tanti in rete, dove volendo ti basta sostituire i valori con quelli del Saturn V (considerando che per lo stadio 1, ma poi per i successivi il discorso si ripete, tutto quello che gli sta sopra è carico utile/pagante, come vedrai nelle dispense o altrove), ma in questo c'è un esempio di dimensionamento di massima, giusto per farsi un'idea vaga di cosa c'è in primissima approssimazione dietro lo studio di un razzo.
www.polismanettoni.altervista.org/alterp...itazionebistadio.pdf
Qualcosa in più sui propellenti che non guasta mai
amslaurea.unibo.it/5197/1/distefano_vittorio_tesi.pdf
E se volessi scendere ancora più in profondità, ma davvero tanto
Apollo systems description-vol 2 www.ibiblio.org/apollo/Documents/19710065502.pdf
Design of liquid rocket engine ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19710019929.pdf
Quello che potevo fare in questo poco tempo (in realtà, qualche bella oretta, vedo
Ciao!
Accedi al sito per partecipare alle discussioni.
innanzitutto chiedo scusa, non era nelle mie intenzioni indurre i partecipanti a sacrificare le ore notturne per fornire arricchimenti, per quanto preziosi.
In effetti hai ragione nell'osservare:
"Innanzitutto, ad occhio, visto che forse non se n'è accorto nessuno, ci dovrebbe essere un errore di battitura nella serie relativa alle percentuali che hai postato, non mi torna la dinamica della progressione numerica nel secondo valore, che penso si avvicini più al 70% che al 60%. Non è che abbia importanza, ma nel caso tu dovessi ripostare la discussione altrove ti consiglierei di controllare prima."
L'errore di battitura c'è stato, poiché ho scritto 62,2% anziché 69,2%, come avrei dovuto. Tuttavia dopo, nell'eseguire la somma che dà 4,613%, ho preso il valore 69,2% e quindi il valore 4,613% non è da correggere e le mie deduzioni successive restano invariate.
Non ti ho più seguito quando hai osservato riguardo alla funzioni svolte dal Terzo Stadio, il modulo S-IVB:
"Tra prima e seconda accensione, in totale, sono stati consumati 214 x 147 + 212 x 346 = 31458+73352 = 104810 kg cioè quasi 105 ton., per cui direi che ci siamo. Ci sono tonnellate da consumare per il prima e ci sono per il dopo, visto che è l'S-IVB a fornire la spinta per il Trans lunar injection. Non vi è un'erogazione aggiuntiva ed ipotetica in corsa, come sostieni, era previsto che si accendesse di nuovo una seconda volta utilizzando il propellente residuo, dimensionato alla bisogna più un certo margine di sicurezza minimo per via del peso aggiuntivo."
Quando ho calcolato l'energia necessaria alla Trans Lunar Injection, cioè quella per portare il solo gruppo MCS+LEM verso la Luna (pari a 1.369.906 MJ, contenuti in ipotetiche 87 t di propellenti), non ho considerato nel gruppo anche S-IVB con la sua massa residua, che tu stesso indichi in 73,352 + 10 = 83,352 t. Ho detto provocatoriamente che un angelo con le sue ali si sarebbe dovuto portare dietro il fardello di 87 t oltre ad altre 10 t di serbatoio, perché altrimenti ci sarebbero volute ben più di 87 t di propellenti per dare l medesima accelerazione anche a S-IVB prima del distacco finale dopo i 346 secondi da te ricordati.
Ufficialmente si è dichiarato proprio questo, cioè che durante la TLI lo stadio S-IVB era attaccato al gruppo MCS+LEM, cosa peraltro ovvia, dato che doveva dargli la spinta.
Però così i conti continuano a non tornare.
Qui approfitto anche per far notare che l'energia chimica dei propellenti in tutti i miei ragionamenti, anche precedenti, è stata generosamente considerata come perfettamente convertibile in energia propulsiva con un'efficienza pari al 100%, a prescindere dal tipo di motore e dalla sue condizioni contingenti di esercizio, e quindi ho anche supposto il massimo effetto Oberth. Eppure anche così i conti non tornano.
Accedi al sito per partecipare alle discussioni.
- Cum grano salis
-

- Offline
- Senior Member
-

Registered
- Se l'avrei saputo, mo' te l'imparavo ;-)
guarda che non ti devi scusare proprio di niente
Tornando a noi, io sono tignoso di natura se un problema mi fa incazzare, e non mollo l'osso come farebbe un cane rabbioso : mi devi abbattere
Quindi, siccome anche stanotte posso fare tardi (per l'ultima volta
Dunque...mi sembra di aver capito che alla fine della fiera a te non torna il discorso dell'energia cinetica necessaria per passare dall'orbita bassa alla TLI. La bufera di vento di oggi mi ha portato alla mente un concetto sepolto e probabilmente detto da un mio professore : quando si ha a che fare con razzi, orbite, masse, spinte e velocità, MAI parlare solo in termini di energie varie, se non alla fine dei giochi o solo ed esclusivamente quando servono davvero e dove servono davvero.
Vediamo se è vero, davvero. (oggi troppo vino di Pasquetta, mi sa...)
Andiamo innanzitutto dall'oste a vedere cosa dice del suo vino buono, e cioè il peso del CSM (quindi CM + SM) e del LEM.
CSM = 28.801 kg che arrotondo a 28.800 kg
nssdc.gsfc.nasa.gov/nmc/spacecraft/display.action?id=1969-059A
The Apollo 11 CSM mass of 28,801 kg was the launch mass including propellants and expendables, of this the Command Module (CM 107) had a mass of 5557 kg and the Service Module (SM 107) 23,244 kg.
LEM = 15.103 kg che arrotondo a 15.100 kg
nssdc.gsfc.nasa.gov/nmc/spacecraft/display.action?id=1969-059C
The lunar module was a two-stage vehicle designed for space operations near and on the Moon. The spacecraft mass of 15103 kg was the total mass of the LM ascent and descent stages including propellants (fuel and oxidizer). The dry mass of the ascent stage was 2445 kg and it held 2376 kg of propellant. The descent stage dry mass (including stowed surface equipment) was 2034 kg and 8248 kg of propellant were onboard initially.
La struttura dell'S-IVB abbiamo visto che era 10.000 kg ed il carburante poi consumato per il TLI era 73.352 kg, che arrotondo a 73.500 kg.
Totale S-IVB = 83.500 kg
Quindi, ricapitolando, nell'orbita bassa abbiamo S-IVB+CSM+LEM e cioè 83.500 + 28.800 + 15.100 = 127.400 kg
Abbiamo visto che la velocità era di 7.793 m/sec.
Vediamo quant'è questa benedetta energia cinetica in orbita bassa, che chiamo Ec1
Ec1 = 0,5 * 127.400 * 7.793 * 7.793 / 1.000.000 = 3.868.555 MJ
Accendiamo i motori, ci fumiamo 73.500 kg di propellente in 5 minuti buoni, e raggiungiamo tutti insieme, ancora uniti come prima i 10.834 m/sec.
Ora vediamo alla fine della TLI che energia cinetica abbiamo, e che chiamo Ec2
Ec2 = 0,5 * (127.400-73.500) * 10.834 * 10.834 / 1.000.000 = 3.163.271 MJ
Avrai capito che sono già in modalità Cazzeggio mode ON di tarda notte.
Ma porca di quella troia!!! Houston, qui abbiamo un ENORME problema !
Come cazzo facciamo ad avere ora MENO energia cinetica di prima che ci fossimo sparati nel di dietro la bellezza di 73 tonnellate e mezza di propellente in poco più di 5 minuti??
Risposta di Houston : Maaaaa, il freno a mano l'avevate tolto...si??
Panico a bordo.
Buzz : Neil, dove minchia sono andati a finire i 3.868.555 - 3.163.271 = 705.284 MJ di energia, che poi dobbiamo fare la scheda carburante e sono mazzate su mazzate di milioni di dollari se non ci tornano i conti?
Neil : ma 'sto robo spaziale non andava a gasolio, che su 600.000 km andata e ritorno dice che si risparmia un botto pure con l'Iperself invece del Servito?? E poi sono millemila punti sulla tessera fedeltà, che poi mi danno le millemiglia Alitalia o lo zainetto col pallone della Nasa?
Houston : 'sto robo va a gas, coglione! Mo' hai ingrippato nello spazio e so' cazzi tua !!
Cazzeggio mode OFF
Dove sono andati a finire noi lo sappiamo bene, li abbiamo spalmati fra massa di propellente ancora da bruciare che stavamo accelerando e che stava però sempre più diminuendo, ed i 212 kg/sec. (che avevo trovato prima dal report) che stavamo contemporaneamente buttando fuori a manetta nello spazio, aumentando ogni secondo il rapporto Spinta/Peso di cui parlavo.
Ora, che possa essere possibile un fabbisogno addirittura negativo rispetto al fabbisogno doppio di energia del tuo ragionamento, non credo che sia oggetto di discussione fra di noi, perché è più che evidente a questo punto che uno di noi due l'ha sparata bella grossa nello spazio :-)
Ora sono quasi le 5, ed io avevo già fatto in modo di essere libero fino a domani, quindi non ci pensare proprio a me neanche stavolta, l'importante è che almeno per ora mi sono sgravato di 73,5 tonnellate di Idrogeno ed Ossigeno dalla testa, così posso dormire tranquillo che non mi saltano per aria insieme al resto del quartiere :-)
Avrai capito che mi piace scherzare, se posso. Domani vediamo come stanno le cose tornando serio, se ho sballato qualcosa nel ragionamento o se ho cannato miseramente i conti, ok?
Ciao!
Accedi al sito per partecipare alle discussioni.
- kamiokande
-

- Offline
- Premium Member
-

Registered
- Messaggi: 488
- Ringraziamenti ricevuti 158
dove "µ" è la costante gravitazionale planetaria, "r" è la distanza dal centro del corpo celeste ed "a" è il semiasse maggiore dell'orbita.
µ Terra = 3.986E+14
Altitudine = 100 nm = 185 km = 185.0E+03 m
Raggio Terra = 6371.0E+03 m
r = 6371.0E+03 + 185.0E+03 = 6.556E+03 m
considerando che l'orbita bassa era praticamente circolare possiamo considerare a = r = 6.556E+03 m , abbiamo una velocità orbitale V = 7800 m/s ; quindi il Saturn V deve essere in grado di raggiungere una velocità di almeno 7800 m/s per mantenere il S-IVB in un orbita circolare stabile a 185 km di altitudine.
Ora veniamo al calcolo del generato dal lanciatore, usiamo l'equazione semplificata (assenza di attrito e di campo gravitazionale) di Tsiolkovsky
quindi il è la somma dei contributi dei singoli stadi. Nel caso del Saturn V ci sono 3 stadi (quindi n = 3) di cui i dati sono
Isp1 = 263 sec Impulso specifico del primo stadio S-IC
M1s = 2957800 kg Massa totale del lanciatore
M1e = 797800 kg Massa totale del lanciatore - Massa di propellente consumato dal 1mo stadio
Isp2 = 421 sec Impulso specifico del secondo stadio S-II
M2s = 667800 kg Massa totale del 2ndo stadio + 3zo stadio + payload
M2e = 211700 kg Massa totale del 2ndo stadio + 3zo stadio + payload - Massa di propellente consumato dal 2ndo stadio
Isp3 = 421 sec Impulso specifico del terzo stadio S-IVB
M3s = 171600 kg Massa totale del 3zo stadio + payload
M3e = 140200 kg Massa totale del 3zo stadio + payload - Massa di propellente consumato dal 3zo stadio (prima accensione)
Il primo impulso specifico appare insolitamente basso, in genere i razzi a RP-1 e LOX hanno un Isp di circa 300, ma comunque questo è il dato indicato e questo ho usato. L'equazione di Tsiolkovsky ci da un di 8960 m/s , che però è approssimata in eccesso. Occorre ora valutare i negativi dovuti alla gravità ed alla resistenza aerodinamica, che sono definiti dalla formule
dove è l'angolo tra l'asse del Saturn V e la verticale locale (per definire la componente del peso da vincere, che è massima quando l'angolo è 90° ovvero con il razzo a perpendicolo rispetto al suolo), "D" è la resistenza aerodinamica ed "m" è la massa del razzo. Per ricavare l'angolo possiamo usare per esempio i dati relativi al lancio di Apollo 11 APOLLO/SATURN V POSTFLIGHT TRAJECTORY AS-505 , da cui ho ricavato l'angolo in funzione del tempo
mentre per la resistenza aerodinamica ho usato questi due grafici
home.kpn.nl/panhu001/Saturn_V/Saturn_V_i...lo_perform_char.html
Dal primo ho ricavato la massa al variare del tempo, dal secondo ho ricavato la pressione dinamica che convertita in pascal e moltiplicata per un coefficiente di resistenza (Cd) di 0.5 (il Cd di un cono, considerato conservativamente costante) dà la resistenza aerodinamica. Dalle formule che ho indicato prima e dai grafici sopra riportati si ottiene una variazione di velocità di -1593 m/s per la gravità (considerata conservativamente costante), e -71 m/s per la resistenza aerodinamica.
La velocità finale raggiunta dal Saturn V è quindi 7296 m/s, mancherebbero all'appello circa 501 m/s che non sono poi molti. Considerando approssimazioni e conservativismi, nonché il fatto che il terzo stadio aveva combustibile combustibile sufficiente ad accelerare ulteriormente fino ai 7800 m/s richiesti (lasciando propellente sufficiente al TLI), direi quindi che, a meno di errori commessi dal sottoscritto, il Saturn V aveva teoricamente la capacità di portare il suo payload dove ci è stato detto ed alla velocità che ci è stata detta. Questo non vuol dire che ne fosse veramente in grado, per essere sicuri di ciò andrebbe analizzato tutto il progetto per evidenziarne eventuali errori e limiti, cosa che credo vada ben oltre le capacità di chi frequenta questo forum.
"La stampa è morta" (Egon Spengler - Ghostbuster)
Accedi al sito per partecipare alle discussioni.
- DanieleSpace
-

- Offline
- Senior Member
-

Registered
- Una volta ero certo. Ora sono pieno di dubbi
- Messaggi: 379
- Ringraziamenti ricevuti 65
Tuttavia ogni volta che facciamo / fai calcoli, si prende sempre per buoni dei dati NASA.
LORO i calcoli li hanno sicuramente fatti per bene ed è possibile che abbiano alterato i valori di massa / capacità di carburante proprio in funzione dell'energia richiesta.
Il razzo era davvero alto quanto dichiarato ? Pesava davvero quanto dichiarato ? Riusciva davvero a trasportare quanto dichiarato ?
Dal punto di vista concettuale non posso obiettare nulla ma dal punto di vista del metodo, fa sempre sorridere quando si verifica la versione di un potenziale bugiardo, prendendo per buone le informazioni fornite dallo stesso.
Una teoria del complotto è ridicola solo quando sono ridicoli i suoi moventi.
Accedi al sito per partecipare alle discussioni.
- Cum grano salis
-

- Offline
- Senior Member
-

Registered
- Se l'avrei saputo, mo' te l'imparavo ;-)
E' pur sempre una velocità di 1.836 km/hr che manca all'appello (una velocità da 'leggero' caccia supersonico) e che manca alla quantità di moto/energia cinetica di svariate decine di tonnellate per stare su e non ricadere a peso morto. Non so se per l'amico MO62 sarebbe sufficiente per mettersi il cuore in pace, ma io non ci dormirei la notte se volessi sostenere a tutti i costi la mia tesi, prima di arrendermi eventualmente all'evidenza.
Fortunatamente ci viene in aiuto ricordare quello che avevo scritto prima
Quindi, senza andare troppo per il sottile andando a verificare che effettivamente il Saturn V abbia seguito perfettamente una traiettoria parallela alla linea immaginaria a latitudine costante sotto di lui, citando Wikipedia...la Terra, pur considerata fissa, sta ruotando su se stessa, quindi al momento della partenza il razzo ha una sua velocità tangenziale che è funzione della latitudine del punto di lancio, motivo per cui si cerca di massimizzare questa velocità cercando di partire da luoghi quanto più vicini all'equatore, puntando poi la traiettoria di volo verso Est, quindi in verso positivo alla rotazione [...] Quindi, sfuttando quanto più possibile la velocità tangenziale di partenza (che all'equatore è di circa 465m/s), alla velocità orbitale di riferimento che dobbiamo ottenere spendendo energia possiamo e dobbiamo togliere la velocità di partenza che già abbiamo in partenza per il solo fatto di ruotare insieme alla Terra.
[N.d.R. vabbé, più che la spinta in Newton, è solo la velocità, ma ci basta il senso del discorso]La spinta verso est della rotazione della Terra è circa 405 m/s
it.wikipedia.org/wiki/Cape_Canaveral_Air_Force_Station
it.wikipedia.org/wiki/Complesso_di_lancio_39
Quindi ci rimane che 510 - 405 = 105 m/sec. e cioè un più ragionevole 378 km/hr nelle approssimazioni, roba da primissime fasi iniziali di volo di un B747 vuoto o di un normale aereo di linea di massa paragonabile all'ultimo stadio, che già è più vicino ai margini di tolleranza/sicurezza del dimensionamento della quantità di propellente che si possono ricavare dal report post volo
pag.97 (prima accensione)
che sono, a 214 kg/sec, 727,6 kg di propellente consumato in più del previsto, praticamente l'1% di quello che poi sarà consumato per il TLI.S-IVB burn duration was 147,1 seconds which was 3.4 seconds more than predicted
Insomma, considerando che i ragionamenti in questi casi si fanno sul kg in più o in meno, sembra poco ma non lo è, a questi livelli.
Però, di contro, a pag.106 (seconda accensione)
Anche in questo caso vengono fatte considerazioni sul fatto che i discostamenti percentuali tra il dato previsto e quello reale rientravano nelle tolleranze.S-IVB second burn duration was 346,9 seconds which was 1,7 seconds less tha predicted
Alla fine, pur nel conteggio di massima, quello che hanno consumato in più prima se lo sono ritrovato più o meno poi.
Quindi, chiuso anche il discorso 'velocità', direi che in base a tutte le considerazioni ed i calcoli, adesso non rimane che aspettare l'onesta opinione di MO62 al riguardo.
Ma, come dicevo
Andiamo innanzitutto dall'oste a vedere cosa dice del suo vino buono
i numeri li forniscono pur sempre loro.
Quindi il mio interesse nel verificare se si tratti di una bugia ben costruita o meno, si è sempre rivolto ai dettagli, dando per scontato che almeno sui numeri non fossero così ingenui come lo sono stati nelle pezze che hanno messo sulle foto, e che mai potevano immaginare che anni dopo si potessero vedere facilmente con un semplice pc da casa.
Per esempio, dopo aver ragionato su questa questione, mi è venuto in mente che gli astronauti dovessero necessariamente avere il modo di affrontare i bisogni corporali anche sulla Luna. E gli spazi e la privacy...quelli erano, non è che la potevano fare fuori dietro un cespuglio, se gli scappava la piccola, o peggio, la grossa
E quindi mi son messo ad indagare un minimo se e come anche questo aspetto fosse stato preso in considerazione, ed in che modo.
Beh, vero o no che sia, devo ammettere che, se fosse, sono stati bravi.
Guarda caso, mi sono capitati fra le mani proprio due articoli recenti
www.ilpost.it/2019/04/04/luna-cacca-astronauti-apollo/
www.vox.com/science-and-health/2019/3/22...on-poop-mars-science
Altra cosa : si parla spesso delle ridottissime capacità informatiche dell'Apollo (ed anche di quelle degli Shuttle), il che è vero per tutta una serie di motivi, oltre al fatto che i processori dovevano essere tali da poter resistere alle radiazioni senza dare dati (bit) sballati.
E quindi, mi son domandato, in quegli anni, quello che c'era a Terra come pianificazione e supporto informatico, cosa poteva essere in concreto, al di là di quello che si può leggere sulla descrizione dei centri di calcolo di allora nei testi? Potevo farmene un'idea, oltre a quello che si poteva vedere in 2001 Odissea nello spazio?
Avevo pure questa curiosità, e devo dire di essere rimasto sopreso, personalmente non ne avevo idea che si potessero fare certe cose nel '68, pur avendo visto e letto dell'IBM & co. o degli esordi molto successivi di Steve Jobs e Steve Wozniak.
The incredible machine (1968)
Accedi al sito per partecipare alle discussioni.
Dunque all’inizio della TLI, secondo quanto dichiarato dalla NASA, entrambi avevano la velocità di orbita bassa pari a 7.793 m/s e al distacco entrambi dovevano aver raggiunto quella di 10.834 m/s.
Calcoliamo allora l’energie cinetiche, all’inizio della TLI (Ec1) e alla fine (Ec2), del blocco formato dal gruppo CSM+LEM e dal S-IVB a secco (serbatoi vuoti), cioè ipotizziamo di nuovo che un angelo segua questo blocco da vicino ed eroghi magicamente, con una pistola nelle prese di carico del S-IVB, i flussi dei due propellenti via via necessari al suo motore.
Ec1 = 0,5*(28.800+15.100+10.800)*7.793*7.793 = 1.660.989 MJ
Ec2 = 0,5*(28.800+15.100+10.800)*10.834*10.834 = 3.210.221 MJ
L’incremento di energia cinetica è pari alla loro differenza e cioè a 1.549.323 MJ
Poiché il potere calorifero dell’idrogeno è di 142 MJ/kg, detto incremento di energia cinetica deve derivare da almeno 10,910 t di idrogeno combinate con 87,281 t di ossigeno, poiché 8 è il rapporto delle masse da combinare nella combustione che produce acqua H2O (peso atomico idrogeno 1, peso atomico ossigeno 16). Totale 98,191 t di propellenti, nel giusto rapporto, necessari all’angelo per riuscire a compiere la TLI.
Sempre la NASA ha dichiarato che sul S-IVB, dopo il parziale utilizzo della scorta di propellenti per raggiungere l’orbita bassa, per la TLI rimanevano disponibili solo 73,352 t in un rapporto tra ossigeno liquido e idrogeno liquido che non era certo pari a 4,84, come quello predisposto al decollo (87,200t / 18,000t), ma un po’ di più, perché nel frattempo parte dell’idrogeno era stato espulso incombusto, allo scopo di mantenere fredda la rimanente parte della scorta pressurizzata. Comunque non era salito a 8, e se anche lo fosse, 73,352 t sono meno delle 98,191 t necessarie alla TLI.
Ricordo infine che in questo calcolo si è ipotizzata la presenza dell’angelo, cioè non si è tenuto conto che la massa del S-IVB all’inizio della presunta TLI in realtà comprendeva anche le 73,352 t di propellenti, che dovevano essere accelerate insieme al suo contenitore, dunque in realtà servivano ben più di 98,191 t.
Non vedo ancora come si possa affermare che grossomodo 73,352 t erano sufficienti alla presunta TLI.
Accedi al sito per partecipare alle discussioni.
- kamiokande
-

- Offline
- Premium Member
-

Registered
- Messaggi: 488
- Ringraziamenti ricevuti 158
Infatti, come ho detto alla fine del mio post precedente, non possiamo sapere se il Saturn V fosse davvero in grado di portare in orbita terrestre e poi lunare il CSM ed il LEM, ma siccome questo thread è nato dall'affermazione che basta qualche calcolo matematico per dimostrarne l'impossibilità, ho voluto dimostrare che ciò è falso. Non avevo molti dubbi sulla questione, se il progetto di massima del razzo avesse mostrato limiti così evidenti chiunque all'interno del progetto se ne sarebbe accorto. L'idea che alla NASA non siano in grado di fare simili calcoli, anche solo per avere un idea di massima di cosa serva er arrivare sulla Luna e tornare, è decisamente ingenua. Poi da qui a costruire macchine in grado di fare quello che i calcoli dicono c'è un abisso. Il calcolo, come ho dimostrato, può farlo una persona sola, il progetto e la costruzione del Saturn V, del CSM e del LEM ha richiesto migliaia di persone.
@ MO62
Usando le formule che ho mostrato sopra si può calcolare quale sia la velocità orbitale per raggiungere con una manovra alla Hohmann la Luna. La distanza media tra la Terra e la Luna è di circa rf = 3.84E+08 m (384000km), quindi un'eventuale orbita che raggiunga la Luna ha un semiasse pari a (ri + rf)/2Non vedo ancora come si possa affermare che grossomodo 73,352 t erano sufficienti alla presunta TLI.
a_TLI = (6.556E+03 + 3.84E+08)/2 = 195.5E+06 m
Dove ri = 6.556E+03 m è l'orbita di partenza che ho calcolato in precedenza. Usando la formula della velocità orbitale che ho riportato
Sapendo che r = ri e che a = a_TLI si ricava che la velocità necessaria per avere un'orbita stabile che possa arrivare alla luna è di 10934 m/s, siccome la velocità orbitale iniziale è circa Vi = 7800 m/s (calcolata in precedenza), abbiamo che la differenza di velocità necessaria per cambiare orbita (da un'orbita circolare intorno alla Terra, ad una fortemente ellittica che porti ad incrociare l'orbita lunare) è di circa 3134 m/s (come avevo detto due post fa). Usando l'equazione di Tsiolkovsky con i seguenti dati
Isp = 421 sec Impulso specifico del terzo stadio S-IVB
Mi = 140200 kg Massa totale del 3zo stadio + payload - Massa di propellente consumato dal 3zo stadio (prima accensione)
Me = 140200 kg - 71068 kg = 69132 kg Mi - propellente consumato
Si ottiene 2920 m/s, considerando che la manovra utilizzata non era una manovra di Hohmann, che la distanza da coprire è minore perché basta arrivare alla sfera di influenza della Luna, e che non tutto il propellente è stato utilizzato, dobbiamo ancora una volta osservare che la manovra era assolutamente fattibile.
"La stampa è morta" (Egon Spengler - Ghostbuster)
Accedi al sito per partecipare alle discussioni.